相机模型与标定笔记

发表于 更新于 分类于 阅读次数： 本文字数： 6.4k 阅读时长 ≈ 6 分钟
大概说明了相机成像投影，针孔模型和鱼眼模型，以及标定的基本原理。

针孔模型的坐标系投影

img
img

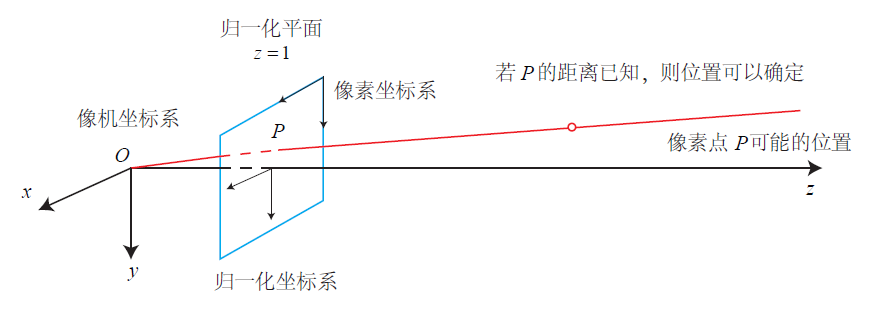
世界坐标系 -> 相机坐标系 -> 归一化平面 -> 像素坐标系

世界坐标系 -> 相机坐标系（外参）

\[ P_c=RP_w+t=\begin{bmatrix}R&t\\0&1\end{bmatrix}P_w=TP_w= \begin{bmatrix} X\\Y\\Z \end{bmatrix} \]

相机坐标系 -> 归一化平面

img
img

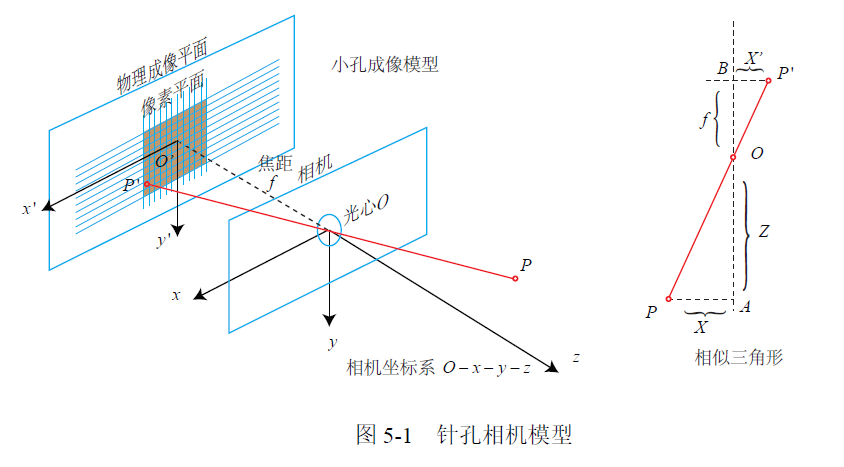
如上图所示，\(X'\) 为归一化平面坐标，\(X\) 为相机坐标系坐标，\(f\) 为焦距（通常单位是毫米 mm）。根据相似三角形： \[ \begin{aligned} \begin{cases} X'=f \frac XZ \\ Y'=f \frac YZ \end{cases} \end{aligned} \] 此时已将归一化平面翻转（非倒像），否则 \(X'\) 与 \(Y'\) 需取负。

归一化平面 -> 像素坐标系

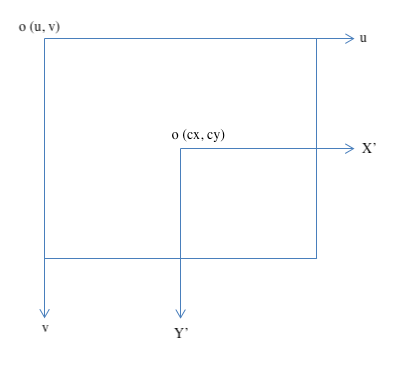
截屏2021-11-18 16.16.12
截屏 2021-11-18 16.16.12

像素坐标系通常从图像左上角开始

设在 \(X'\) 方向：\(1\,pix=dx\,mm\) （毫米转像素）;

在 \(Y'\) 方向：\(1\,pix=dy\,mm\)

则： \[ \begin{cases} u=\frac {1}{dx}X'+c_x\\ v=\frac {1}{dy}Y'+c_y \end{cases} \] 与前一步合并一下： \[ \begin{cases} u=f_x\frac XZ+c_x\\ v=f_y\frac YZ+c_y \end{cases} \] 转换成矩阵形式： \[ \begin {aligned} \underbrace {\begin {pmatrix} u\\v\\1 \end {pmatrix}}_\text {其次坐标} = \frac 1Z \begin {pmatrix} f_x&\gamma&c_x\\ 0&f_y&c_y\\ 0 &0&1 \end {pmatrix} \underbrace {\begin {pmatrix} X\\Y\\Z \end {pmatrix}}_\text {非其次坐标} =\frac 1ZKP \end {aligned} \] 其中： \[ \begin{cases} f_x=\frac f{dx}\\ f_y=\frac f{dy} \end{cases} \] \(\gamma\) 描述的是两个坐标轴的偏转。

\(K\) 称为内参矩阵

对于齐次坐标，尺度因子（这里指距离 Z）不会改变坐标值的；与光心位于同一直线的所有点在归一化平面上是同一个投影点。

畸变矫正

畸变主要分为了径向畸变和切向畸变：

径向畸变

img
img

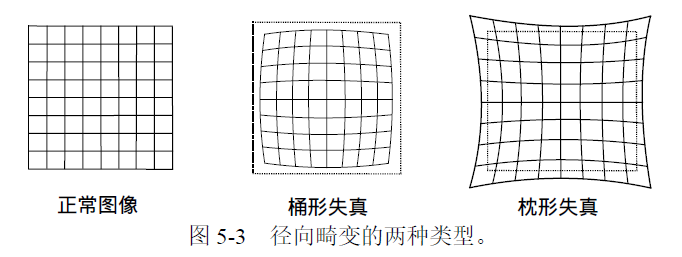
畸变模型使用多项式来描述如下： \[ \begin{aligned} x_{distort}=x_n\cdot(1+k_1r^2+k_2r^4+k_3r^6)\\ y_{distort}=y_n\cdot(1+k_1r^2+k_2r^4+k_3r^6) \end{aligned} \] 其中 \(x_n\) 和 \(y_n\) 为归一化坐标： \[ \begin{cases} x_n = \frac XZ \\ y_n = \frac YZ \end{cases} \] 注意他们并不是归一化平面上的坐标，与其相差了一个因子 \(f\)。 \[ r=\sqrt{x_n^2+y_n^2} \] 一般多项式取到前三项，即三个径向畸变参数 \(k_1\),\(k_2\),\(k_3\)。

对于畸变很小的中心区域，　主要起作用的是 \(k_1\)；

对于畸变较大的边缘区域，主要起作用的是 \(k_2\)；

对于畸变很大的鱼眼相机，可以加入 \(k_3\) 来表示；

image-20211118171045569
image-20211118171045569

切向畸变

img
img
img
img

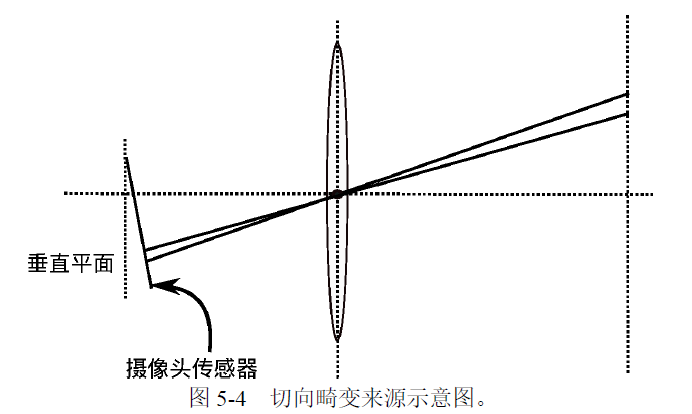
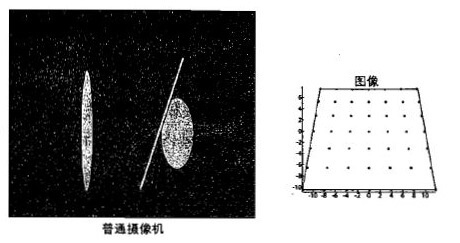
通常是透镜与像平面没有严格平行导致。

畸变模型描述如下： \[ \begin{aligned} x_{distort}=x_n+2p_1x_ny_n+p_2(r^2+2x^2) \\ y_{distort}=y_n+p_1(r^2+2y^2)+2p_2x_ny_n \end{aligned} \] image-20211118171850959

畸变矫正

我们合并一下可以得到： \[ \begin{cases} x_{distort}=x_n\cdot(1+k_1r^2+k_2r^4+k_3r^6)+2p_1x_ny_n+p_2(r^2+2x^2)\\ y_{distort}=y_n\cdot(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2x_ny_n \end{cases} \] 通常记相机畸变参数为： \[ disCoffes = [k_1,k_2,p_1,p_2,k_3] \]

去畸变程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <opencv2/opencv.hpp>
#include <string>

using namespace std;

string image_file = "../test.png";   // 请确保路径正确

int main(int argc, char **argv) {

    // 本程序需要你自己实现去畸变部分的代码。尽管我们可以调用OpenCV的去畸变，但自己实现一遍有助于理解。
    // 畸变参数
    double k1 = -0.28340811, k2 = 0.07395907, p1 = 0.00019359, p2 = 1.76187114e-05;
    // 内参
    double fx = 458.654, fy = 457.296, cx = 367.215, cy = 248.375;

    cv::Mat image = cv::imread(image_file,0);   // 图像是灰度图，CV_8UC1
    int rows = image.rows, cols = image.cols;
    cv::Mat image_undistort = cv::Mat(rows, cols, CV_8UC1);   // 去畸变以后的图

    // 计算去畸变后图像的内容
    for (int v = 0; v < rows; v++)
        for (int u = 0; u < cols; u++) {

            double u_distorted = 0, v_distorted = 0;
            double x_distorted = 0, y_distorted = 0;
            // TODO 按照公式，计算点(u,v)对应到畸变图像中的坐标(u_distorted, v_distorted) (~6 lines)
            // start your code here
            double x = (u - cx)/fx;
            double y = (v - cy)/fy;
            double r_2 = x*x + y*y;
            x_distorted = x*(1+k1*r_2+k2*r_2*r_2)+2*p1*x*y+p2*(r_2+2*x*x);
            y_distorted = y*(1+k1*r_2+k2*r_2*r_2)+p1*(r_2+2*y*y)+2*p2*x*y;
            u_distorted = fx*x_distorted+cx;
            v_distorted = fy*y_distorted+cy;
            // end your code here

            // 赋值 (最近邻插值)
            if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < cols && v_distorted < rows) {
                image_undistort.at<uchar>(v, u) = image.at<uchar>((int) v_distorted, (int) u_distorted);
            } else {
                image_undistort.at<uchar>(v, u) = 0;
            }
        }

    // 画图去畸变后图像
    cv::imshow("image undistorted", image_undistort);
    cv::waitKey();

    return 0;
}

鱼眼相机

鱼眼相机标定不能使用针孔模型，而是使用鱼眼相机模型，见论文：Kannala J, Brandt S S. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28 (8): 1335–1340.

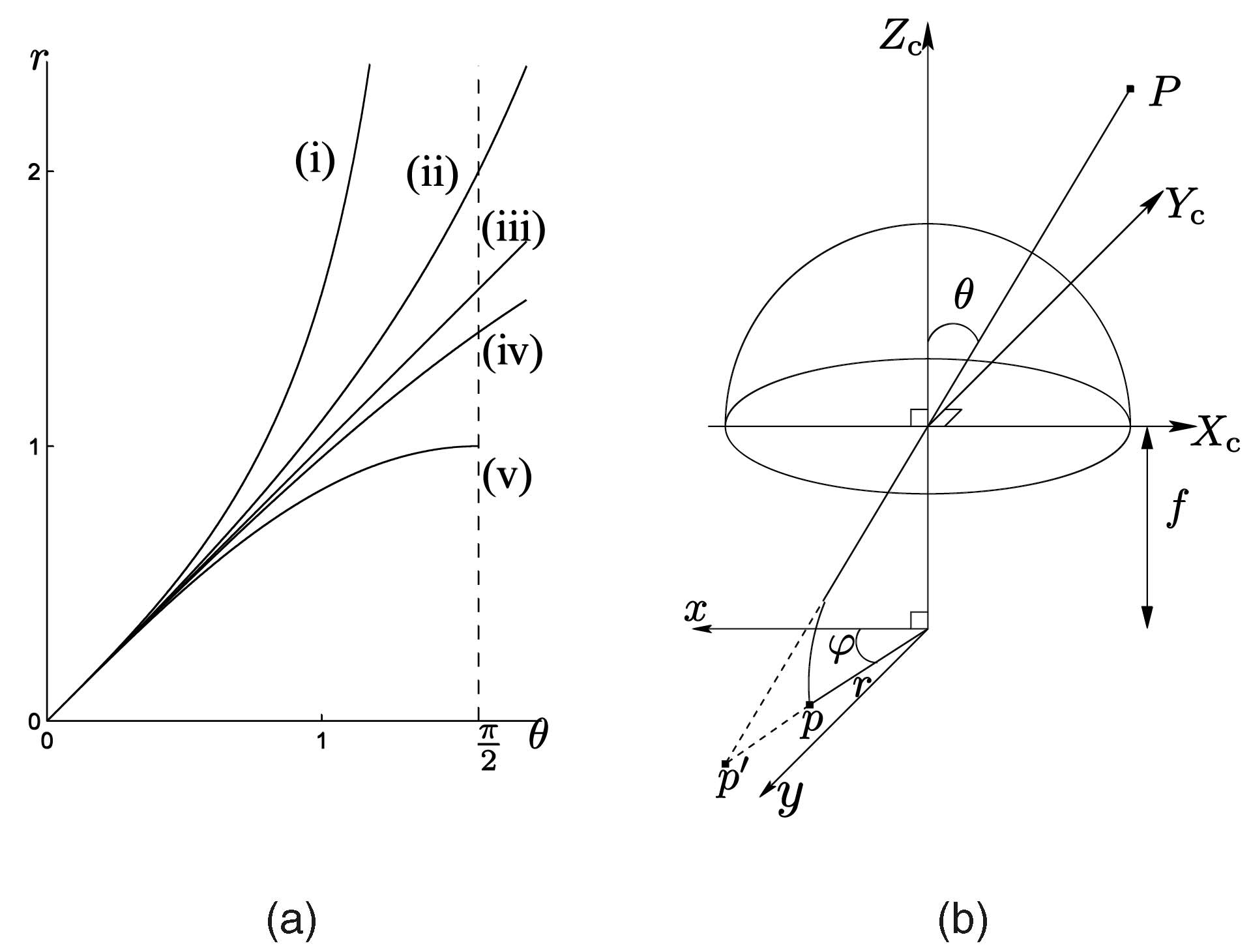
image-20211125162218474
image-20211125162218474

针孔相机可以描述成下述公示： \[ r=f\tan\theta \]

\[ \begin {aligned} \text {外参：} TX_w=\begin {bmatrix} X\\Y\\Z\end {bmatrix} \\ x_n=\frac XZ,\;y_n = \frac YZ \\ r^2 = x^2_n + y^2_n\\ \theta = \arctan (r)\\ \theta_d=k_0\theta+k_1\theta^3+k_2\theta^5+k_3\theta^7+k_4\theta^9\\ x_d = \frac {\theta_d}{r} x_n,\;y_d = \frac {\theta_d}{r} y_n,\\ u = f_xx_d+c_x, v = f_yy_d+c_y \end {aligned} \]

张氏标定法

\[ s\begin{bmatrix}u\\v\\1\end{bmatrix} = A\begin{bmatrix}r_1&r_2&r_3&t\end{bmatrix} \begin{bmatrix}X\\Y\\0\\1\end{bmatrix}\\ A = \begin{bmatrix}c&cs&xH\\0&c(1+m)&yH\\0&0&1\end{bmatrix} \]

我们把世界坐标系设置在标定板上，所以世界坐标中的 Z=0。由于 Z=0，公示化简如下： \[ s\begin{bmatrix}u\\v\\1\end{bmatrix} = \underbrace{\begin{bmatrix}c&cs&xH\\0&c(1+m)&yH\\0&0&1\end{bmatrix}}_K \underbrace{\begin{bmatrix}r_{11}&r_{12}&t_1\\r_{21}&r_{22}&t_2\\r_{31}&r_{32}&t_3\end{bmatrix}} _{\begin{bmatrix}r_1&r_2&t\end{bmatrix}} \begin{bmatrix}X\\Y\\1\end{bmatrix} \]

计算 H

单应矩阵 H： \[ H=\lambda\begin{bmatrix}c&cs&xH\\0&c(1+m)&yH\\0&0&1\end{bmatrix} \begin{bmatrix}r_{11}&r_{12}&t_1\\r_{21}&r_{22}&t_2\\r_{31}&r_{32}&t_3\end{bmatrix} \\ \] 其中 \(\lambda\) 可以是任意的尺度因子

在一张 checkerboard 图像上有 \(I\) 个特征点，我们能生成 \(I\) 条公式： \[ \begin{bmatrix}x_i\\y_i\\1\end{bmatrix}=H\begin{bmatrix}X_i\\Y_i\\1\end{bmatrix} \] 由于 H 有 8DoF（少了一个尺度因子），每一个特征点提供 x 和 y 两个约束，所以一张图至少要有 4 个特征点算 H。

由 H 计算 K

\[ H = \begin{bmatrix}h_1&h_2&h_3\end{bmatrix}=A\begin{bmatrix}r_1&r_2&t\end{bmatrix} \]

由于 Q\(r_1\) 和 \(r_2\) 正交： \[ \begin{cases} r_1^Tr_2=0\\ r_1^Tr_1 = r_2^Tr_2=1 \end{cases}\\ \] 易得两个约束： \[ \begin{cases} r_1 = A^{-1}h_1\\ r_1 = A^{-1}h_1 \end{cases} \;\Rightarrow\; \begin{cases} h_1^TA^{-T}A^{-1}h_2=0\\ h_1^TA^{-T}A^{-1}h_1=h_2^TA^{-T}A^{-1}h_2 \end{cases} \\ \] B 是对称阵，可以表示成 6D 向量 b \[ B=A^{-T}A^{-1}=\begin{bmatrix}B_{11}&B_{12}&B_{13}\\B_{21}&B_{22}&B_{23}\\B_{31}&B_{32}&B_{33}\end{bmatrix}\\ b=\begin{bmatrix}B_{11}&B_{12}&B_{22}&B_{13}&B_{23}&B_{33}^T\\\end{bmatrix} \] 令： \[ h^T_iBh_j=v^T_{i,j}b \\ \text{with}\\v=\begin{bmatrix} h_{i1}h_{j1}&h_{i1}h_{j2}+h_{i2}h_{j1}&h_{i2}h_{j2}&h_{i3}h_{j1}+h_{i1}h_{j3}&h_{i3}h_{j2}+h_{i2}h_{j3}&h_{i3}h_{j3} \end{bmatrix}^T \] 其中一个 H 可以生成一条下述公式： \[ \begin{bmatrix}v^T_{12}\\(v_{11}-v_{22)})^T\end{bmatrix}b=0 \] v 与 H 相关，b 与内参 K 相关。

有 n 张图我们可以得到如下矩阵： \[ \begin{bmatrix}v^T_{012}\\(v_{011}-v_{022)})^T\\...\\ v^T_{n12}\\(v_{n11}-v_{n22)})^T\end{bmatrix}b=Vb=0 \] 强制添加约束 b=1，最小化下述误差： \[ b^*=arg\,\underset b{min}\,||b|| \quad\text{with}\:||b||=1 \] 因为 B 有 5 或 6 个 DoF，我们需要至少 3 个平面。

非线性参数

非线性参数在这里即畸变向量，为图像坐标加上偏移量（畸变模型）： \[ \begin{aligned} \triangle x(x,k,q), \\ \triangle y(y,k,q) \end{aligned} \] 其中 k,q 分别是径向畸变和切向畸变的参数。

代畸变的内参 \(K_a\) 可以表示为： \[ K_a=\begin{bmatrix}1&0&\triangle x(x,k,q)\\ 0&1&\triangle y(y,k,q)\\ 0&0&0\\ \end{bmatrix}K \] 优化以下函数： \[ \underset{(K,k,q,R_t,t_n)}{min}\;\sum_n\sum_i||x_{ni}-\hat{x}(K,k,q,R_t,t_n,X_{ni})||^2 \] \(K\)：内参

\(k\)：径向畸变

\(q\)：切向畸变

\(R_t\)：旋转矩阵

\(t_n\)：平移向量

\(X_{ni}\)：世界坐标

工具

  1. OpenCV
  2. CamOdoCal
  3. Kalibr
  4. Matlab