四旋翼无人机动力学与控制

四旋翼无人机的动力学与控制可以分为两个部分，一部分是上位机控制无人机的推力 \(F\) 和扭矩 \(M\)，另一部分是飞控根据推力和扭矩控制四旋翼的电机。本文主要关注前者的动力学与控制。

运动学

定义惯性系 \(\{\vec{a_1},\vec{a_2},\vec{a_3}\}\) 表示为 {A} 和机体系表 \(\{\vec{b_1},\vec{b_2},\vec{b_3}\}\) 示为 \(\{B\}\)。\(\{B\}\) 在 \(\{A\}\) 的表达为：

\[ R^A_B= \begin{bmatrix} 𝑐\psi 𝑐\theta −𝑠\phi 𝑠\psi 𝑠\theta & −𝑐\phi 𝑠\psi & 𝑐\psi 𝑠\theta +𝑐\theta 𝑠\phi 𝑠\psi \\ 𝑐\theta 𝑠\psi +𝑐\psi 𝑠\phi 𝑠\theta & 𝑐\phi 𝑐\psi & 𝑠\psi 𝑠\theta −𝑐\psi 𝑐\theta 𝑠\phi \\ −𝑐\phi 𝑠\theta & 𝑠\phi & 𝑐\phi 𝑐\theta \end{bmatrix} \]

四旋翼的运动学方程如下：

\[ \text {欧拉角模型} \begin {cases} \dot {\mathbf {p}} = \mathbf {v} \\ \dot {\mathbf {\Theta}} = W \cdot \mathbf {\omega} \end {cases} \\ \text {旋转矩阵模型} \begin {cases} \dot {\mathbf {p}} = \mathbf {v} \\ \dot {\mathbf {R}} = \mathbf {R}[\mathbf {\omega}]_\times \end {cases} \]

其中，\(\mathbf{p}\) 表示四旋翼两个时刻质心位置的向量，\(\mathbf{v}\) 表示 \(\{B\}\) 相对 \(\{A\}\) 的线速度在坐标系 \(\{A\}\) 中的表达。

\(\dot{\mathbf{\Theta}}\) 表示姿态变化率（并无具体对应坐标系，或者说不同轴对应坐标系不同），\(\mathbf{\omega}\) 是坐标系 \(\{B\}\) 下的机体旋转角速度。

\[ \mathbf{\Theta} = \begin{bmatrix} \phi & \theta & \psi \end{bmatrix}^T \]

姿态变化率 \(\dot{\mathbf{\Theta}}\) 与机体角速度 \(\mathbf{\omega}\) 并不相等，其转换关系取决于欧拉角类型，以 ZXY 为例：

\[ \begin{cases} \dot{\phi} = R_Y(\theta) \cdot \mathbf{\omega}_x \vec{b_1} \\ \dot{\theta}=\mathbf{\omega}_y \vec{b_2} \\ \dot{\psi} = R_X(\phi)R_Y(\theta) \cdot \mathbf{\omega}_z \vec{b_3} \end{cases} \]

推得

\[ \begin{bmatrix} \mathbf{\omega}_x \\ \mathbf{\omega}_y \\ \mathbf{\omega}_z \end{bmatrix} = \begin{bmatrix} c\theta & 0 & -c\phi s\theta \\ 0 & 1 & s\phi \\ s\theta & 0 & c\phi c\theta \end{bmatrix} \begin{bmatrix} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{bmatrix} \]

\[ W= \begin{bmatrix} c\theta & 0 & s\theta \\ t\phi s\theta & 1 & -t\phi c\theta \\ -s\theta / c\phi & 0 & c\theta/c\phi \end{bmatrix} \]

注意 \(W\) 并非旋转矩阵，不是齐次矩阵。

动力学

通过牛顿 - 欧拉方程建立动力学模型。由牛顿 - 欧拉方程可知，刚体运动 = 质心的平动 + 绕质心的转动。

\[ m\ddot {\mathbf {p}}=-m\cdot g\vec {a_3}+R^A_B\cdot f\vec {b_3}\quad \text {牛顿方程}\\ I\mathbf {\dot {\omega}}+\mathbf {\omega}\times I\mathbf {\omega}=G_a+\tau\quad \text {欧拉方程} \]

其中，\(f\) 和 \(\tau\) 分别为四旋翼产生的推力和力矩，\(G_a\) 表示陀螺力矩。

陀螺力矩：当电机高速旋转的时候，相当于一个陀螺。高速旋转的陀螺是非常稳定的个体，具有保持自身轴向不变的能力。因此如果有外力想改变陀螺转轴的方向，那么会产生一个陀螺力矩来抵抗这种改变。

单个螺旋桨的陀螺力矩可以表示为：

\[ \begin{aligned} G_{a,k} & = J_{RP}(-1)^k\varpi_k\vec{b_3}\times\omega \\ & = J_{RP}(\omega\times\vec{b_3})(-1)^{k+1}\varpi_k \end{aligned} \]

其中，\(k\) 为电机序号，\(J_{PR}\) 为转子加旋翼的转动惯量，\(\varpi\) 为电机角速度。由于：

\[ \omega\times\vec{b_3}= \begin{bmatrix} \omega_y & -\omega_x & 0 \end{bmatrix}^T \]

所以：

\[ G_{a}= \begin{bmatrix} -J_{PR}\omega_y\varpi_{sum} \\ J_{PR}\omega_x \varpi_{sum}\\ 0 \end{bmatrix}\\ \varpi_{sum} = -\varpi_1+\varpi_2-\varpi_3+\varpi_4 \]

将无人机视为均匀对称的刚体，可以认为转动惯量：

\[ I=\begin{bmatrix} I_x&&\\ &I_y&\\ &&I_z \end{bmatrix} \]

稍作整理：

\[ \ddot{\mathbf{p}}= \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{bmatrix} = \begin{bmatrix} \frac{f}{m}(s\theta c\psi+s\phi c\theta s\psi) \\ \frac{f}{m}(s\theta s\psi-s\phi c\theta c\psi) \\ \frac{f}{m}c\phi c\theta-g \end{bmatrix} \]

\[ \dot{\omega}= \begin{bmatrix} \dot{\omega_x}\\\dot{\omega_y}\\\dot{\omega_z} \end{bmatrix}= \begin{bmatrix} \frac{1}{I_x}[\omega_y\omega_z(I_y-I_z)-J_{RP}\omega_y\varpi_{sum}+\tau_x] \\ \frac{1}{I_y}[\omega_x\omega_z(I_z-I_x)+J_{RP}\omega_x\varpi_{sum}+\tau_y] \\ \frac{1}{I_z}[\omega_x\omega_y(I_x-I_y)+\tau_z] \end{bmatrix} \]

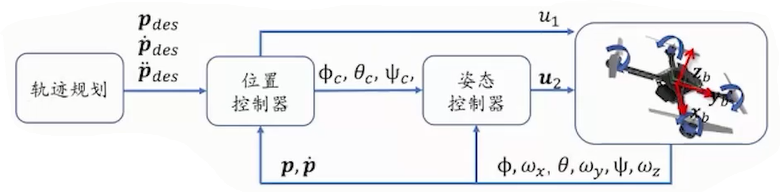
线性控制器

首先进行线性化，假设无人机处于悬停状态，则 \(\phi\) 和 \(\theta\) 趋于 0，\(\frac{f}{m}\) 趋于 \(g\)。

\[ \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{bmatrix} = \begin{bmatrix} g(\theta c\psi+\phi s\psi) \\ g(s\theta \psi-\phi c\psi) \\ \frac{f}{m}-g \end{bmatrix} \]

image-20220719205139467

PID:

\[ \ddot{z_c}=\ddot{z_{des}}+K_{d,z}(z_{des}-z)+K_{d,z}(\dot{z_{des}}-\dot{z}) \]

前馈加 PD

模型：

\[ f=m(g+\ddot{z_c}) \\ \phi_c=\frac{1}{g}(\ddot{x}s\psi-\ddot{y}c\psi) \\ \theta_c=\frac{1}{g}(\ddot{x}c\psi+\ddot{y}s\psi) \]

值得注意的是，\(\psi\) 单独进行控制。

PID：

\[ \dot{\omega}_{x,c}=K_{d,\phi}(\phi_{c}-\phi)+K_{d,\phi}(\omega_{x,c}-\omega_x) \\ \dot{\omega}_{y,c}=K_{d,\theta}(\theta_{c}-\theta)+K_{d,\theta}(\omega_{y,c}-\omega_y) \\ \dot{\omega}_{z,c}=K_{d,\psi}(\psi_{c}-\psi)+K_{d,\psi}(\omega_{z,c}-\omega_z) \]

模型：

\[ \tau = I\mathbf{\dot{\omega}_c}+\mathbf{\omega}\times I\mathbf{\omega} \]

注意此处忽略陀螺力矩。

代码：

function [F, M] = controller(t, s, s_des)

    global params

    m = params.mass;
    g = params.grav;
    I = params.I;

    x_des = s_des(1);
    y_des = s_des(2);
    z_des = s_des(3);
    dx_des = s_des(4);
    dy_des = s_des(5);
    dz_des = s_des(6);

    qua_des = s_des(7:10);
    [row_des, pic_des, yaw_des] = RotToRPY_ZXY(quaternion_to_R(qua_des));

    drow_des = s_des(11);
    dpic_des = s_des(12);
    dyaw_des = s_des(13);

    ddx_des = 0;
    ddy_des = 0;
    ddz_des = 0;

    x = s(1);
    y = s(2);
    z = s(3);
    dx = s(4);
    dy = s(5);
    dz = s(6);
    qua = s(7:10);
    [row, pic, yaw] = RotToRPY_ZXY(quaternion_to_R(qua));
    drow = s(11);
    dpic = s(12);
    dyaw = s(13);

    K_ddx_p = 25;
    K_ddx_d = 12;
    K_ddy_p = 25;
    K_ddy_d = 12;
    K_ddz_p = 70;
    K_ddz_d = 20;
    K_ddrow_p = 400;
    K_ddrow_d = 30;
    K_ddpic_p = 400;
    K_ddpic_d = 30;
    K_ddyaw_p = 300;
    K_ddyaw_d = 25;

    R_ab = [cos(pic), 0, -cos(row) * sin(pic); 0, 1, sin(row); sin(pic), 0, cos(row) * cos(pic)];
    w_xyz = R_ab * [row; pic; yaw];
    w_x = w_xyz(1);
    w_y = w_xyz(2);
    w_z = w_xyz(3);

    ddx = ddx_des + K_ddx_p * (x_des - x) + K_ddx_d * (dx_des - dx);
    ddy = ddy_des + K_ddy_p * (y_des - y) + K_ddy_d * (dy_des - dy);
    ddz = ddz_des + K_ddz_p * (z_des - z) + K_ddz_d * (dz_des - dz);

    row_c = (ddx * sin(yaw) - ddy * cos(yaw)) / g;
    pic_c = (ddx * cos(yaw) + ddy * sin(yaw)) / g;
    yaw_c = yaw_des;

    drow_c = 0;
    dpic_c = 0;
    dyaw_c = 0;

    if (((yaw_c - yaw) >- pi) && ((yaw_c - yaw) < pi))
        d_yaw_c = yaw_c - yaw;
    elseif ((yaw_c - yaw) <= -pi)
        d_yaw_c = yaw_c - yaw + 2 * pi;
    elseif ((yaw_c - yaw) >= pi)
        d_yaw_c = yaw_c - yaw - 2 * pi;
    end

    ddrow = K_ddrow_p * (row_c - row) + K_ddrow_d * (drow_c - drow);
    ddpic = K_ddpic_p * (pic_c - pic) + K_ddpic_d * (dpic_c - dpic);
    ddyaw = K_ddyaw_p * (d_yaw_c) + K_ddyaw_d * (dyaw_c - dyaw);

    F = m * (g + ddz);
    M = I * [ddrow; ddpic; ddyaw] + cross([w_x; w_y; w_z], I * [w_x; w_y; w_z]);

    % F = 1.0; M = [0.0, 0.0, 0.0]'; % You should calculate the output F and M

end