普林斯顿大学算法第一部分
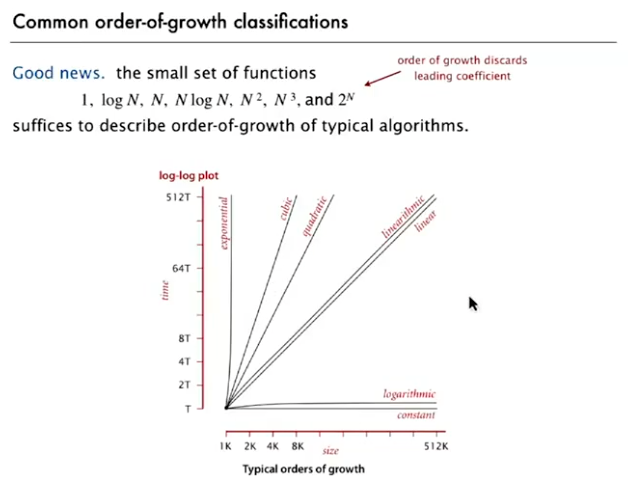

binary search
recurrence:
\[ \begin{aligned} T(N)&\leq T(\frac N2)+1\\ &\leq T(\frac N4)+1+1\\ &...\\ &\leq T(\frac NN) +1+...+1\\ &=1+\log(N) \end{aligned} \]
二分查找解决 3-SUM 问题:
遍历前两个数,查找第三个能让和为 0 的数,复杂度为 N^2logN
Dynamic Connectivity
Quick Find

union 时需要遍历整个 array,改变 id

\(N^2\) 的复杂度是不能容忍的(当算力和数据量同时增长一倍,耗时也会增长一倍)
分析:
- find () 操作的时间复杂度为𝑂(1),因为只需要访问一次 id 数组
- union () 操作的时间复杂度为𝑂(𝑁),因为每一个合并都需要遍历整个 id 数组
- 如果有 M 对连接𝑂(𝑀𝑁),那么构建出所有的分量的时间复杂度为。
Quick Union
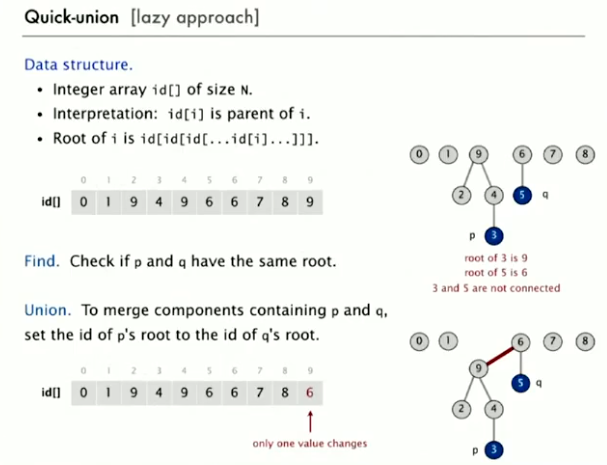
只改变两个需要链接节点的根节点


时快时慢,当树很深的时候,会导致 find 变慢,而每一次 union 都需要 find。
分析:
- 最好情况下,find () 操作的时间复杂度是𝑂(1),最坏情况下,find () 操作的时间复杂度是𝑂(𝑁)
- union () 操作的时间复杂度应该与 find () 操作是一致的。
改进 Weighted Quick Union
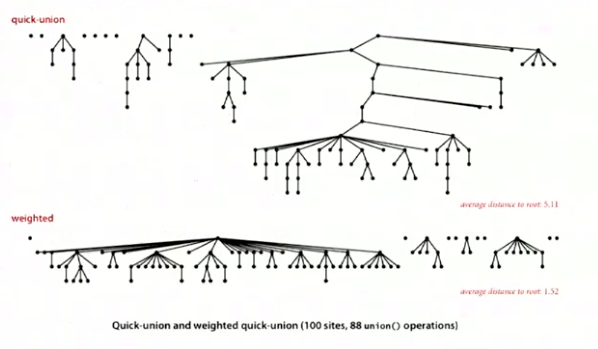
永远将小树的根节点添加到大树的根节点上(大小指的是深度)


为什么是 \(\log(N)\)?
思考 N 个节点时最多有多少层?
| 节点数量 | 高度 |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 2^k=n | k |
如需要扩展到第三层,就需要两个相同的最小的两层结构,即 4*4=8
log 基数为 2
path compression(在寻找 root 节点时做压缩)


Fundamental Data Type
stack

linked-list implementation
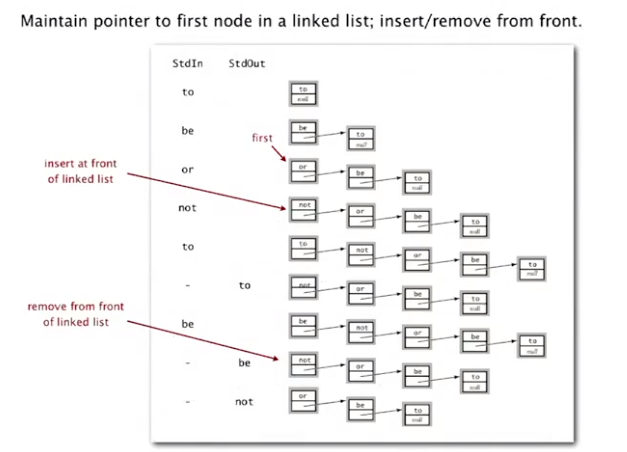
array implementation
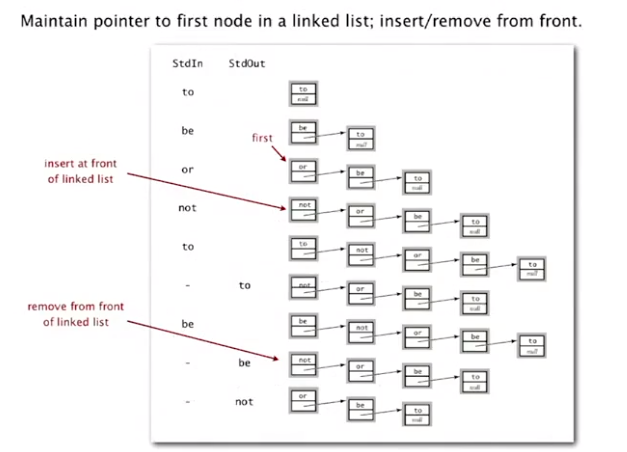
Resizing Arrays
Grow array
单个扩容和两倍扩容的对比:
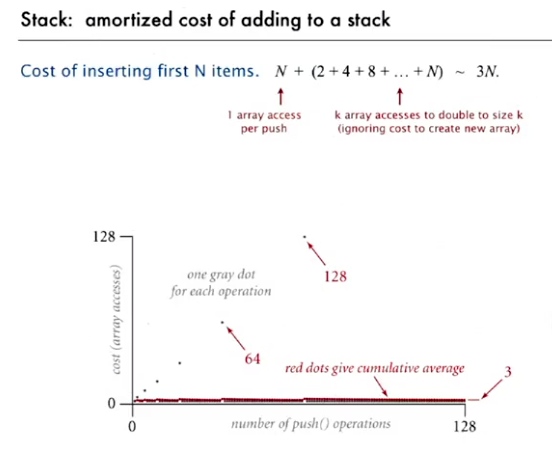
shink arrays

Resizing array vs. linked list

Queues
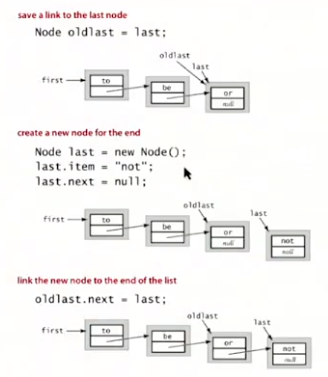
linked-list implementation
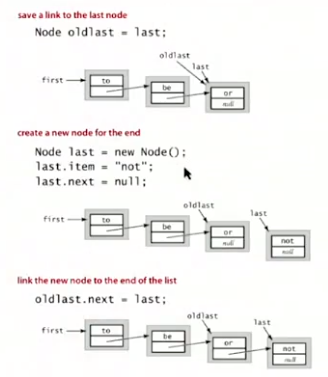
array implementation
Sorting
Sorting Complexity

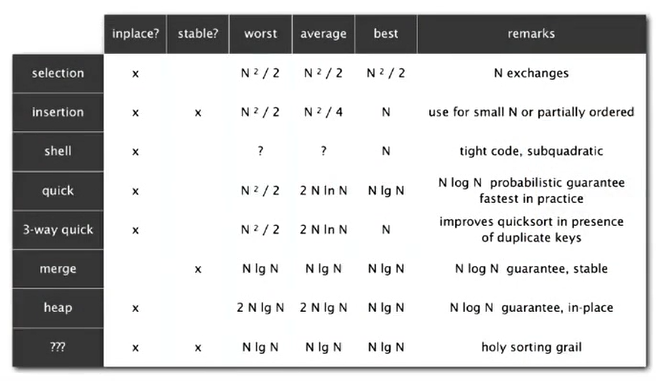
Stability
不打乱原有顺序
Selection Sort
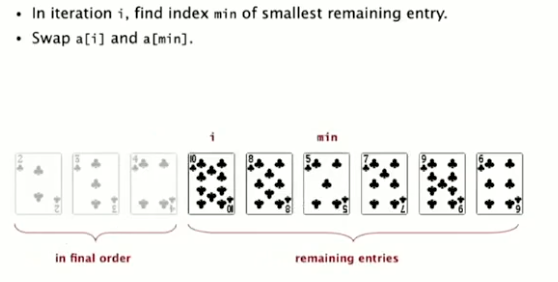
遍历 i,寻找后续最小的元素并交换
implementation:
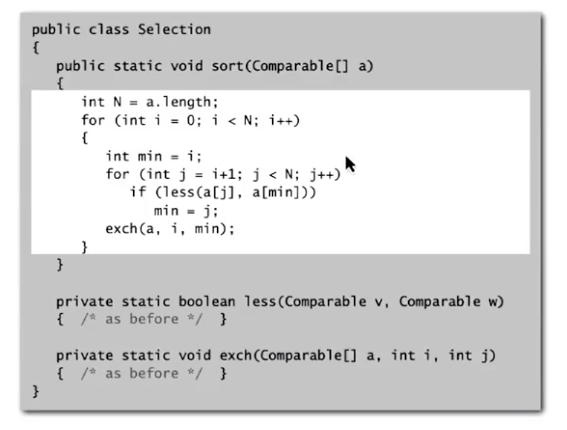
复杂度:
比较次数:\((N-1)+(N-2)+...+1+0\;\sim\;\frac{N^2}2\)
交换次数:\(N\)
Insertion Sort
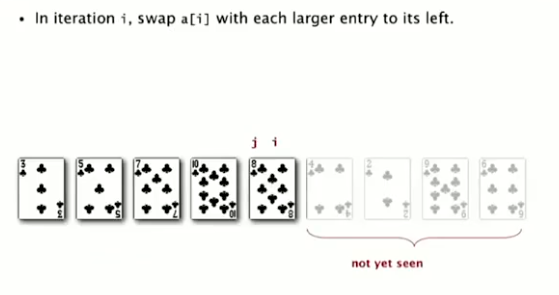
迭代 i,当 i 小于前一个元素时交换,交换后继续判断与前一个元素的大小,如果小于,则继续交换,直到大于为止。
implementaion

复杂度(平均):
比较次数:\(\frac14N^2\)
交换次数:\(\frac14N^2\)
Best case (排好序):
Compares: \(N-1\)
Exchanges: \(0\)
Worst case (倒序):
Compares: \(\frac12N^2\)
Exchanges: \(\frac12N^2\)
Partially-sorted arrays

Insertion sort 在 Partially-sorted arrays 中时间复杂度是线性的
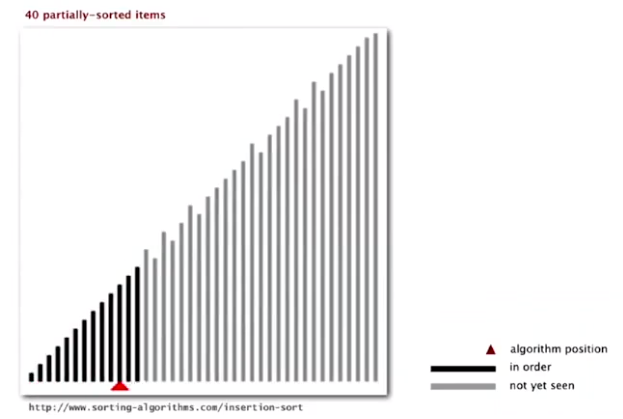
Shell Sort
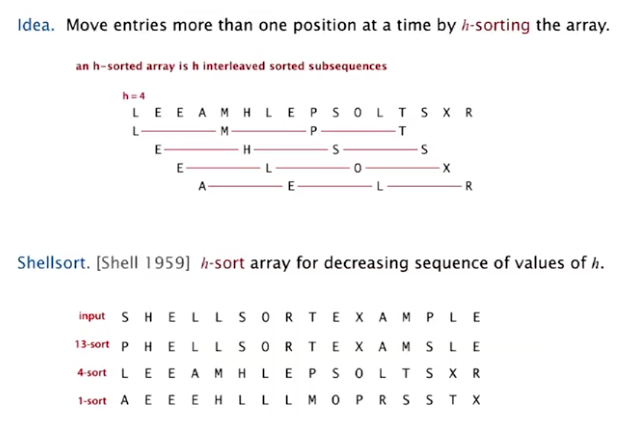
insertion sort with stride length h.
Why insertion sort?
Big increments -> small subarray -> nearly in order

implementation
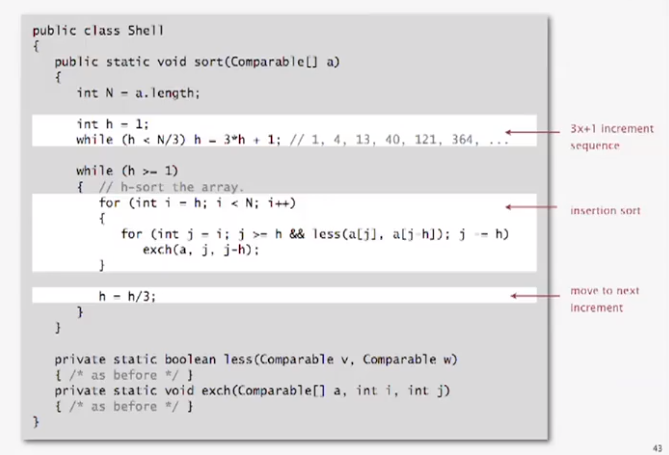
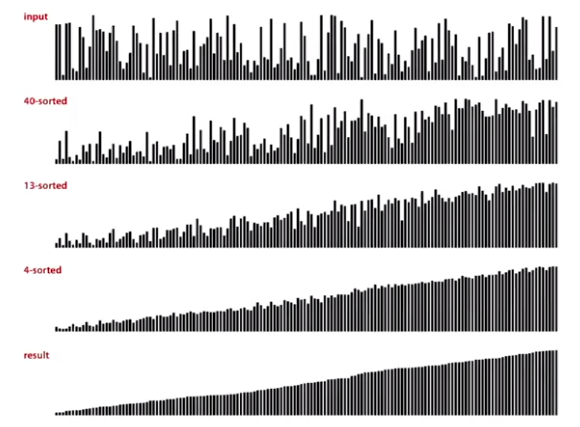
vworst-case:
Compares used: \(O(N^{\frac32})\) (With 3x+1 increments)
Property:
No accurate model. Maybe $N lg N $

Shuffling
Shuffle sort:

Knuth Shuffle:
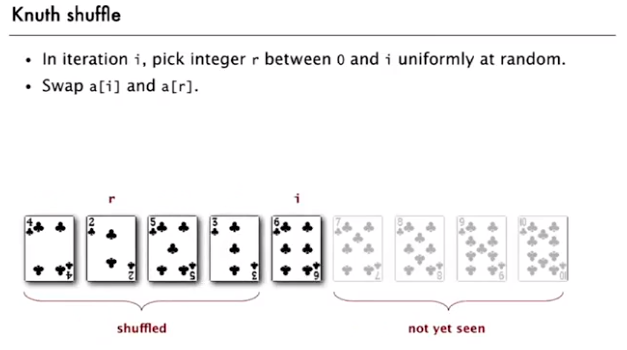

Merge Sort
分治,递归


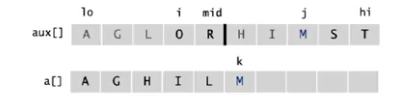
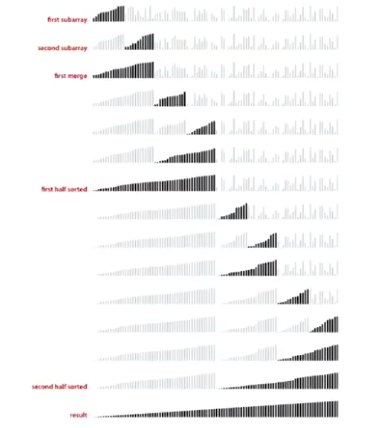
worst case:
Compares: \(NlgN\)
Array accesses: \(6NlgN\)

递归次数:
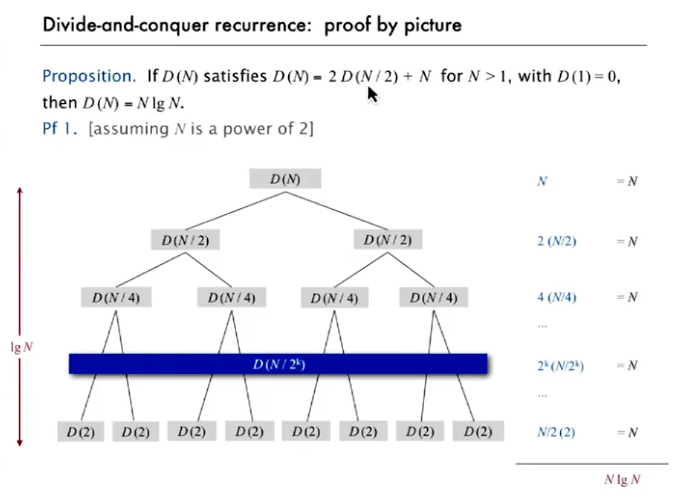
memory: Extra space proportional to N
improvement
The cutoff to insertion sort for 7 items.
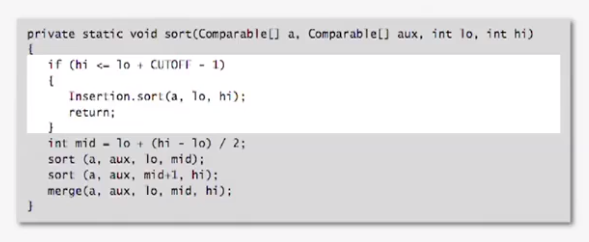
stop merge if already sorted
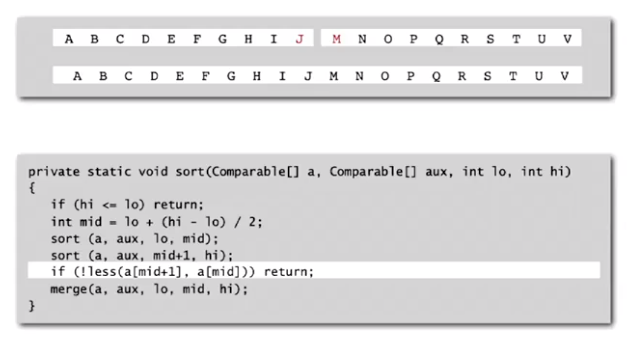
Bottom-up Mergesort
No Recursion Needed!
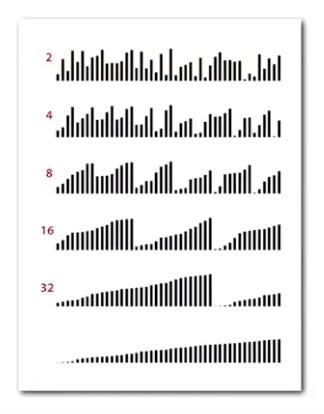
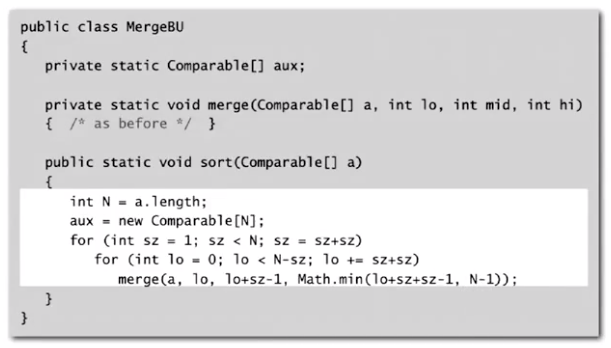
Quick Sort

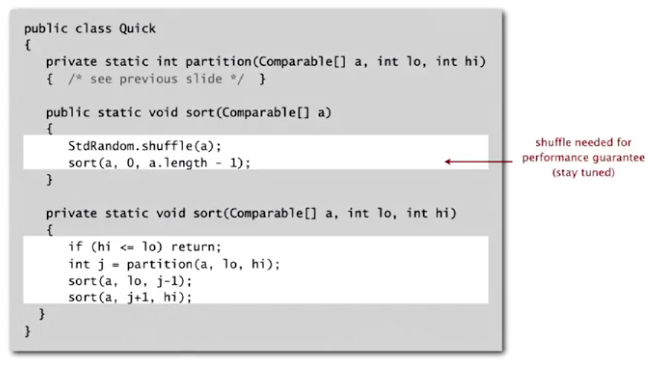


Shuffling is needed for performance guarantee

best case: \(NlgN\)
Worst case: \(\frac12 N^2\)
Quick-select
Given an array of N items, find a \(k^{th}\) smallest item.


Duplicate keys
Mergesort with DUPLICATE KEYS. Always between \(\frac12NlgN\) and \(NlgN\) compares.
Quicksort with DUPLICATE KEYS. goes quadratic.
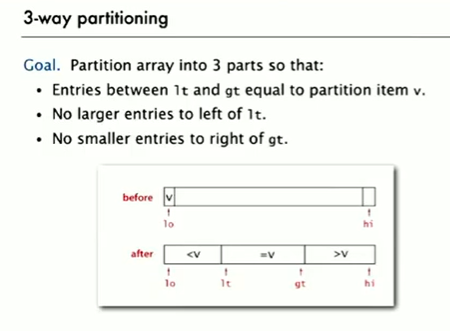

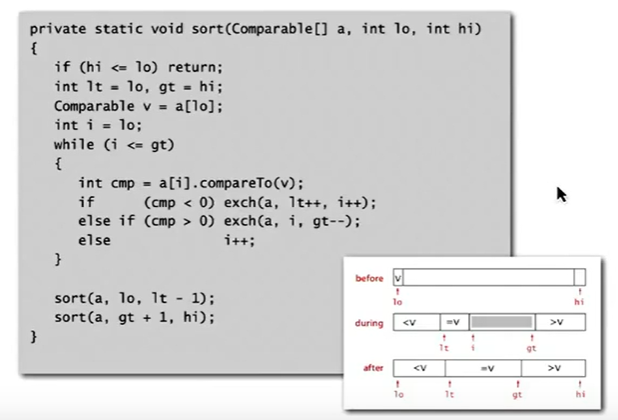

Priority Queue
Find the largest M items in a stream of N items.


Unorder array implementation
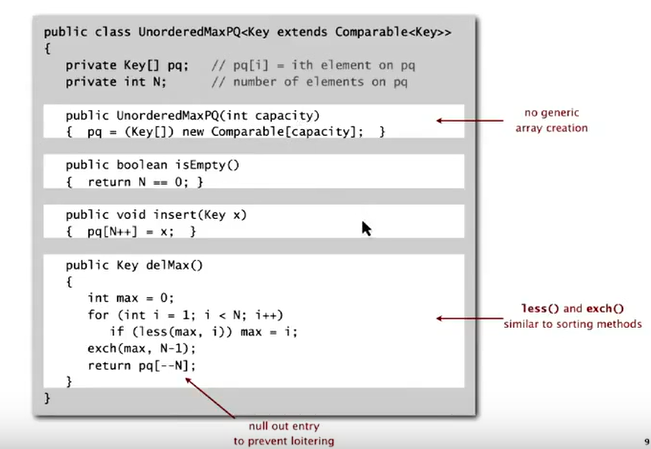
Binary Heaps
Array representation of a heap-ordered complete binary tree.
- keys in nodes.
- Parent’s no smaller than children’s keys.
Array representation:
- indices start at 1.
- Take nodes in level order.
- No explicit links needed!
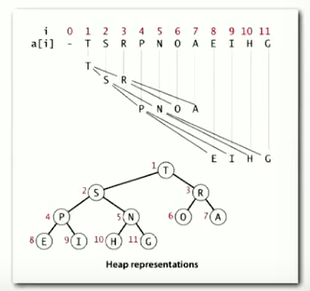
Root: a[1]
Parent of node at k: k/2
Children of node at k: 2k and 2k+1
Minimum-oriented priority queue: Replace less() with greater().
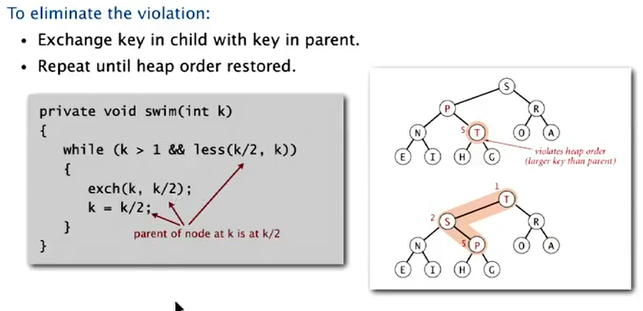
swim
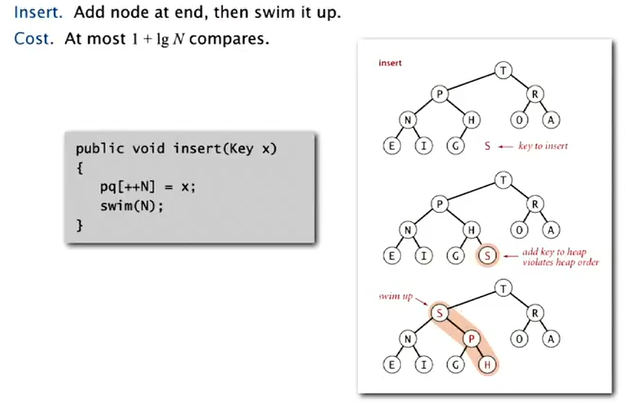
insert
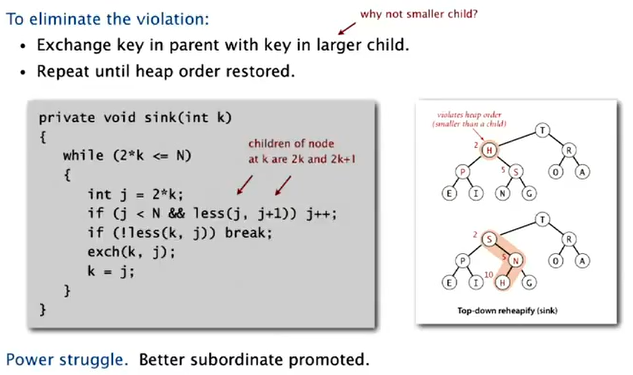
sink
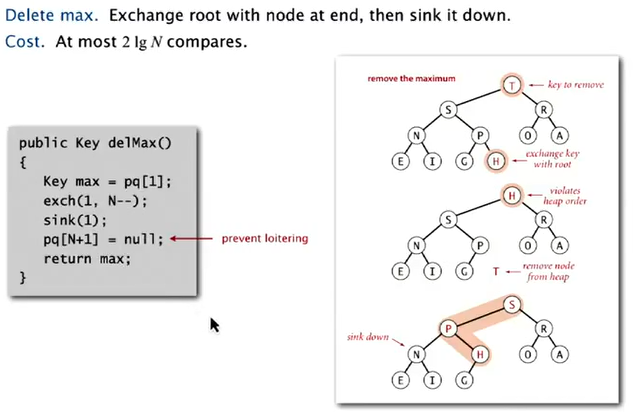
delete
Heap Sort
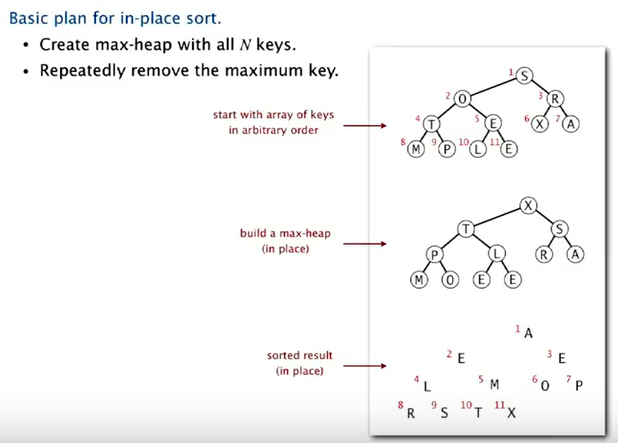
- 从倒数第二排向上从右到左做 sink,构造二叉树。
- 依次取出最大值。

Symbol Tables
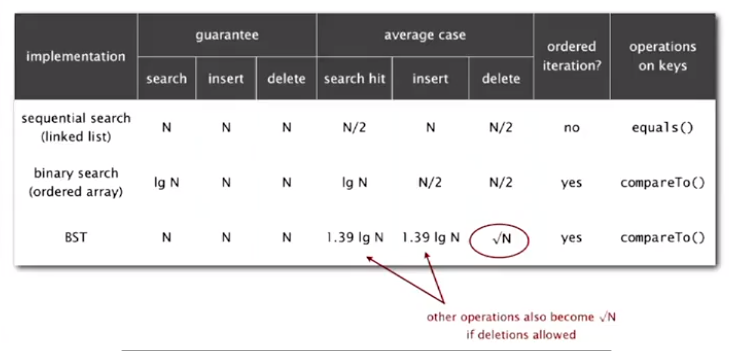
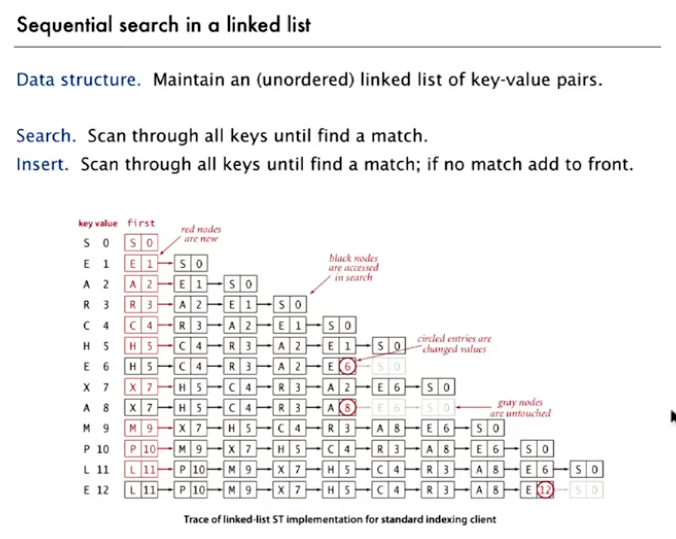
Sequential Search (unordered list):
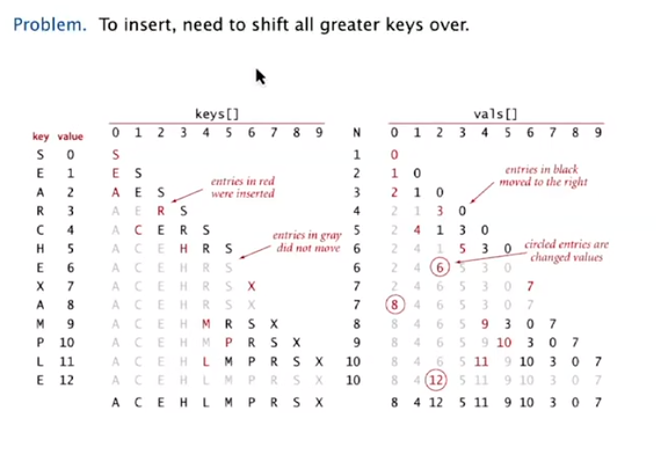
Binary Search (order list)
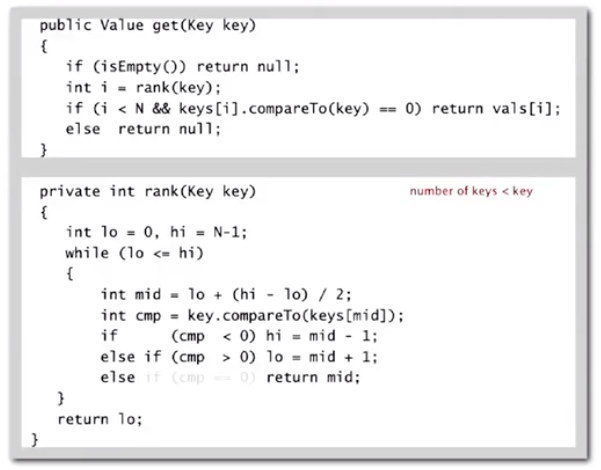
Binary Search Tree (BST)
- Larger than all keys in its left subtree
- Smaller than all keys in its right subtree
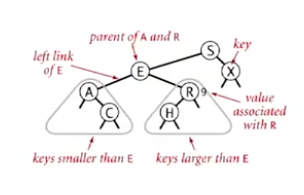
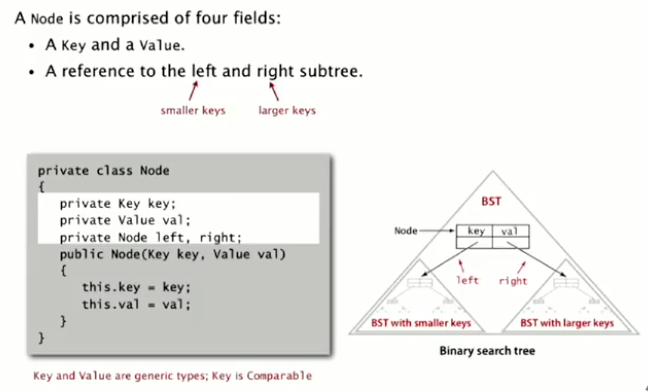
Search

Insert
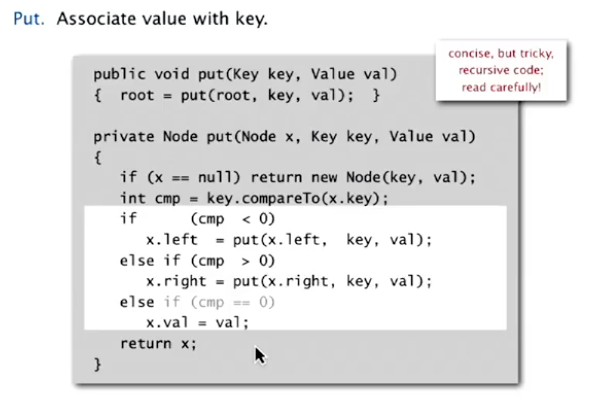
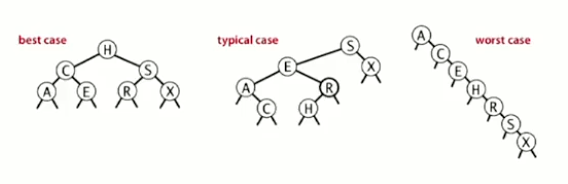
Floor
Largest key less to a given key.
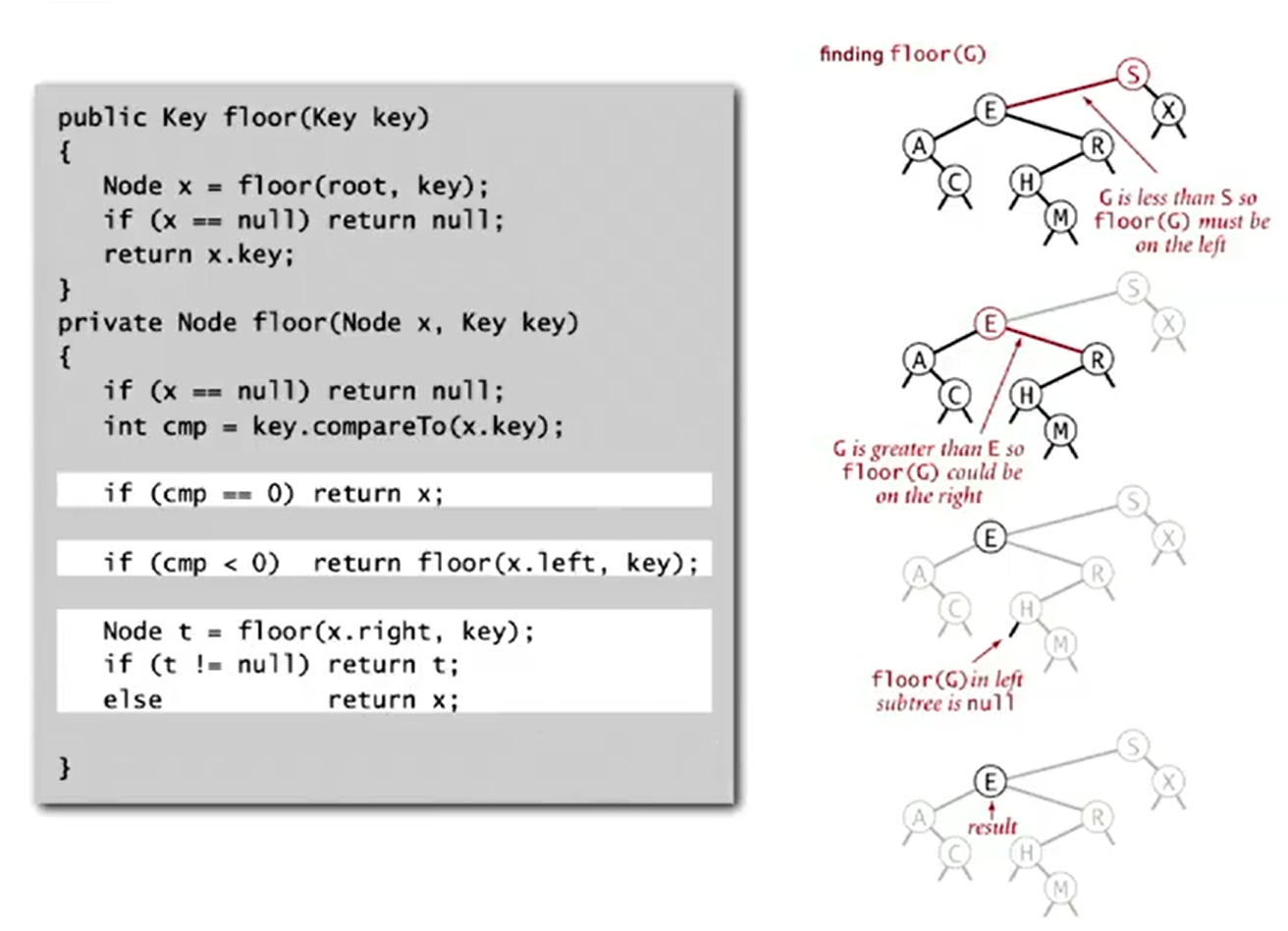
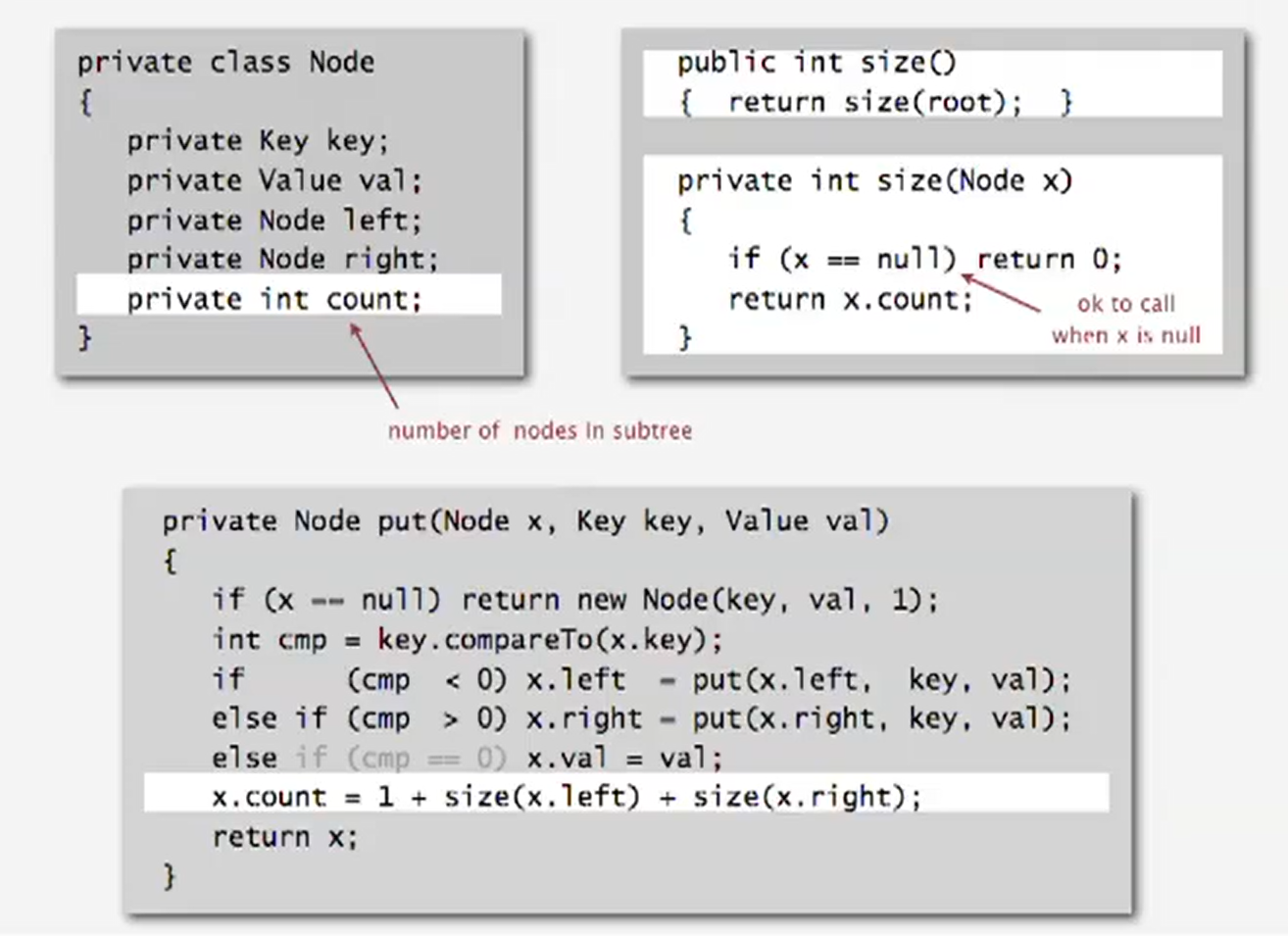
subtree count
In each node, we store the number of nodes in the subtree rooted at that node;
remark. This facilitates efficient implementation of rank() and select()
implementation:
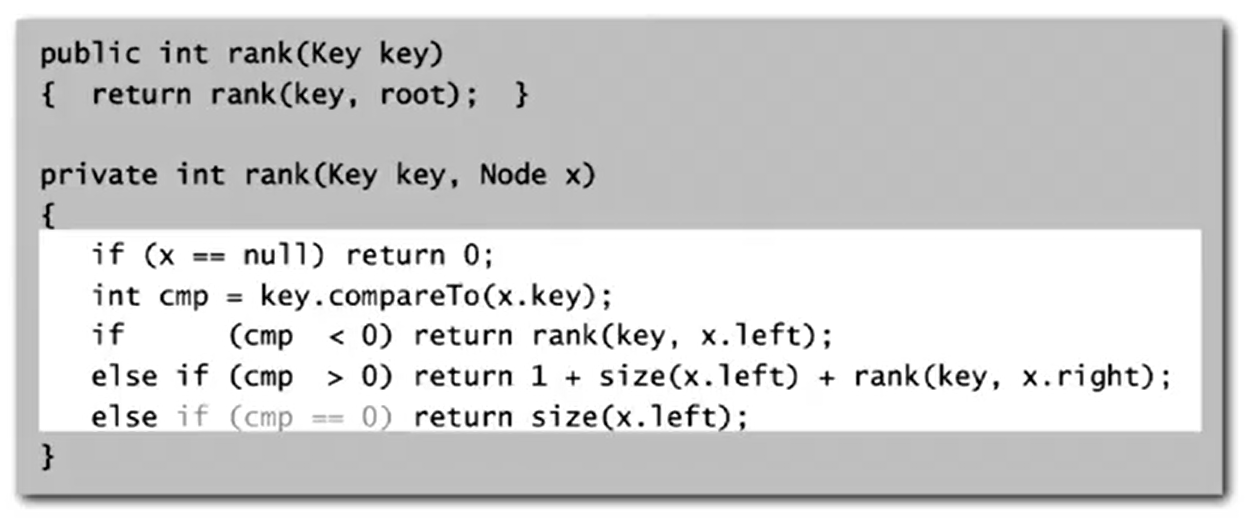
Rank
How much keys < \(k\)
Inorder traversal
from small to large

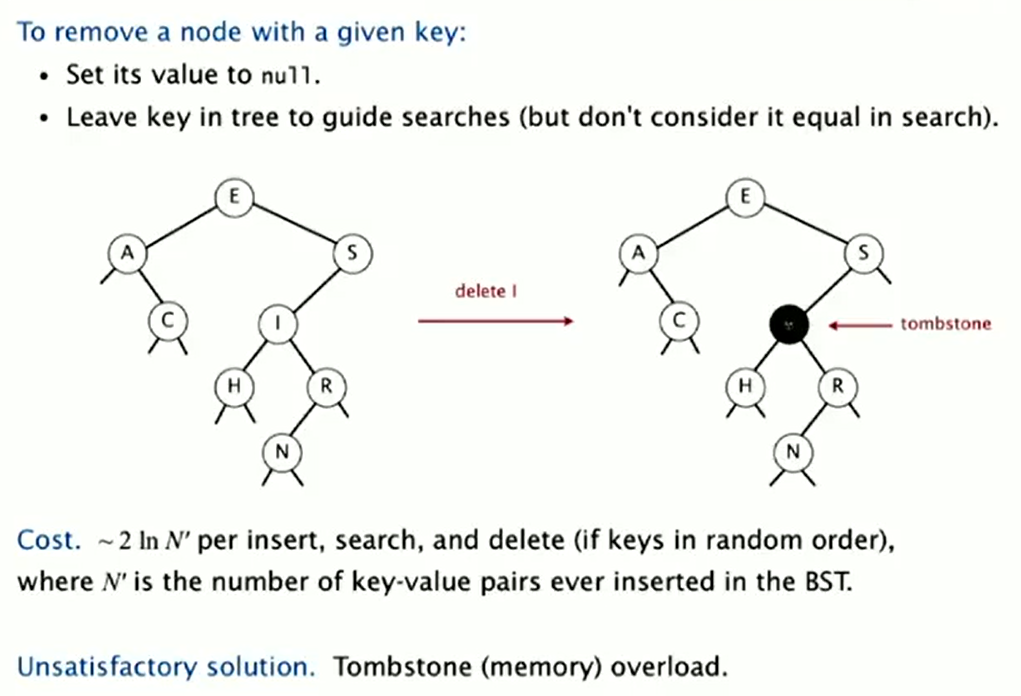
Deletion
Lazy approach (Tombstone)
![image-20220926124150541]()
Hibbard deletion
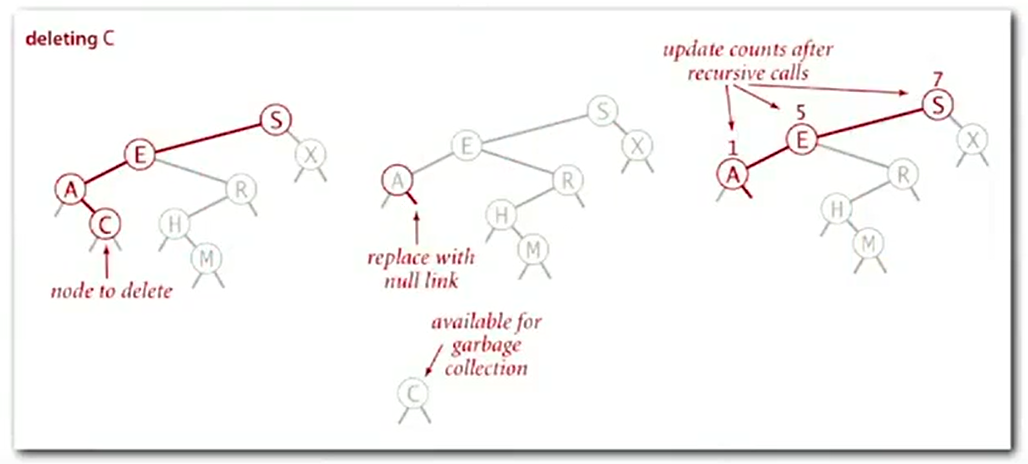
case 0: 0 children
![image-20220926125026950]()
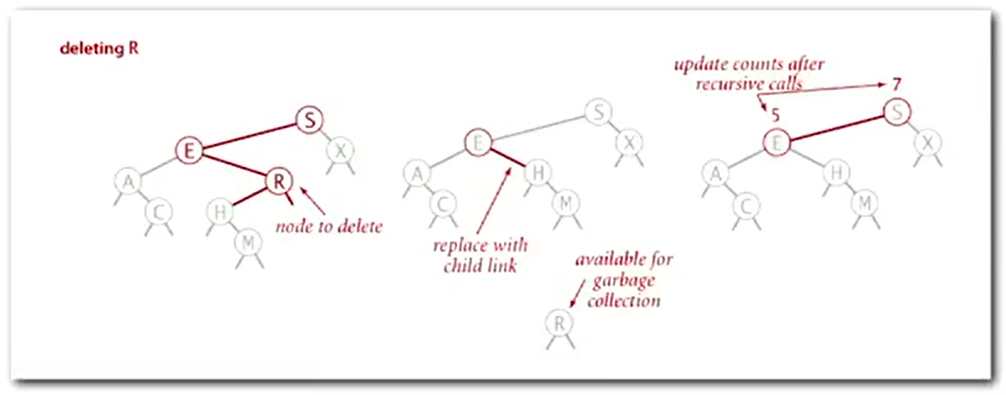
case 1: 1 child
![image-20220926125101190]()
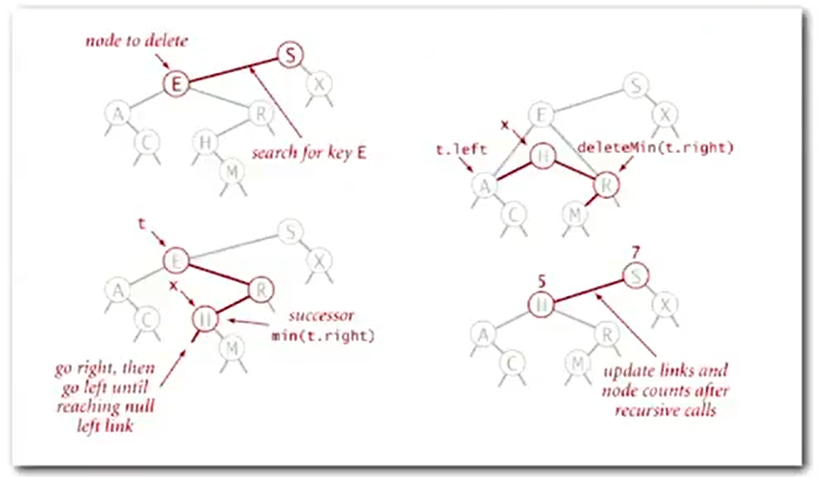
case 2: 2 children
![image-20220926125129935]()
image-20220926125129935
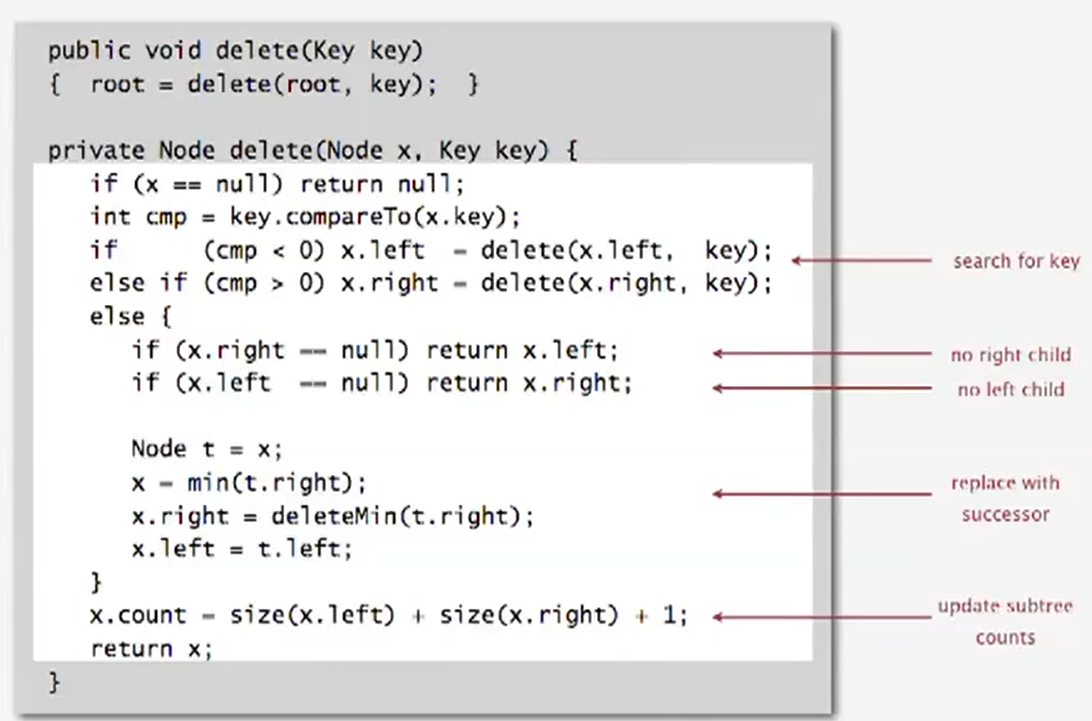
Implementation:
![image-20220926125219834]()
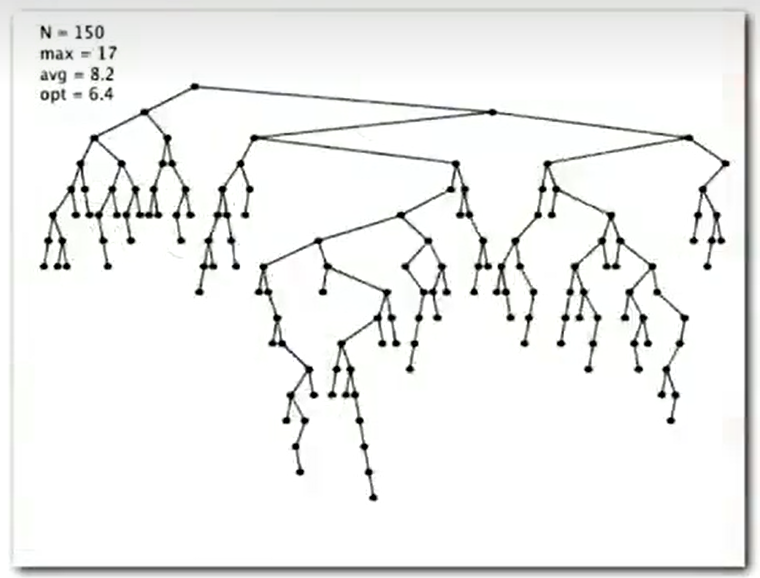
image-20220926125219834 NOT SYMMETRIC:
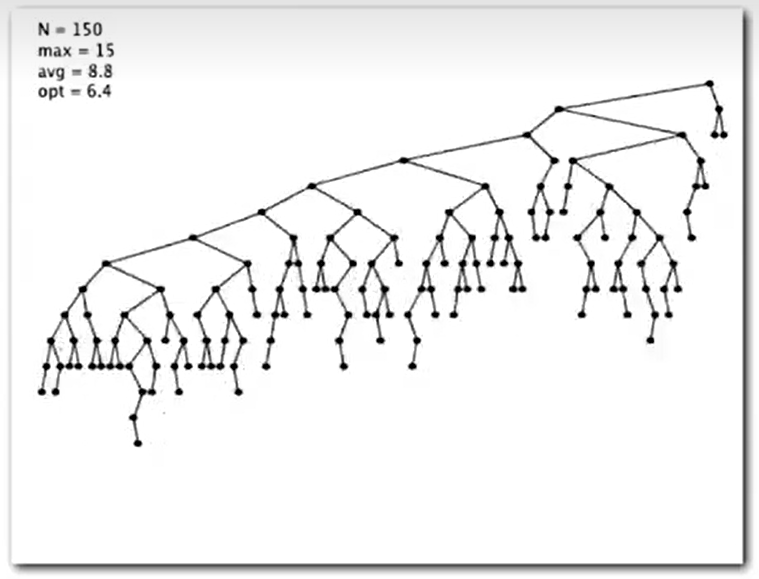
Hibbard algorithm lack of symmetry that tends to lead to difficulties.
![image-20220926125508278]()
image-20220926125508278 ![image-20220926125543012]()
image-20220926125543012
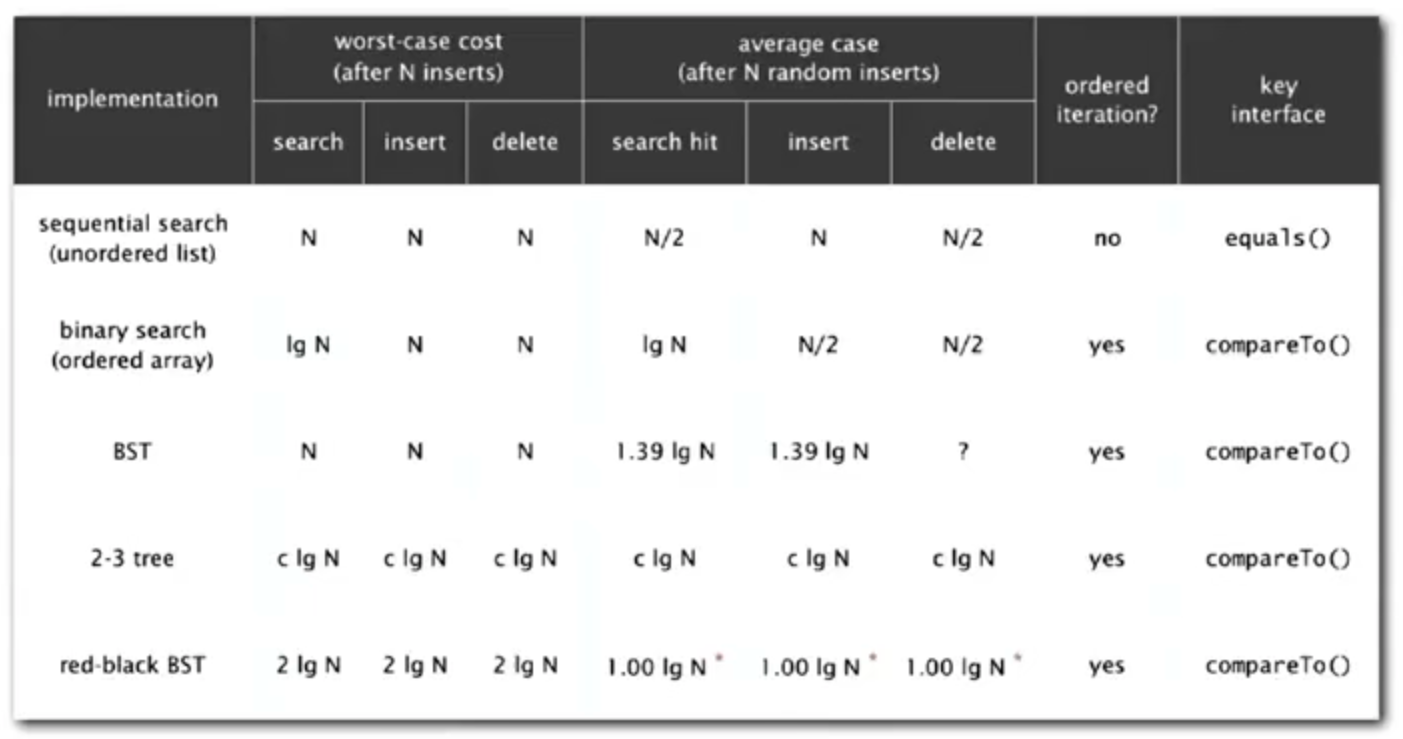
Summary
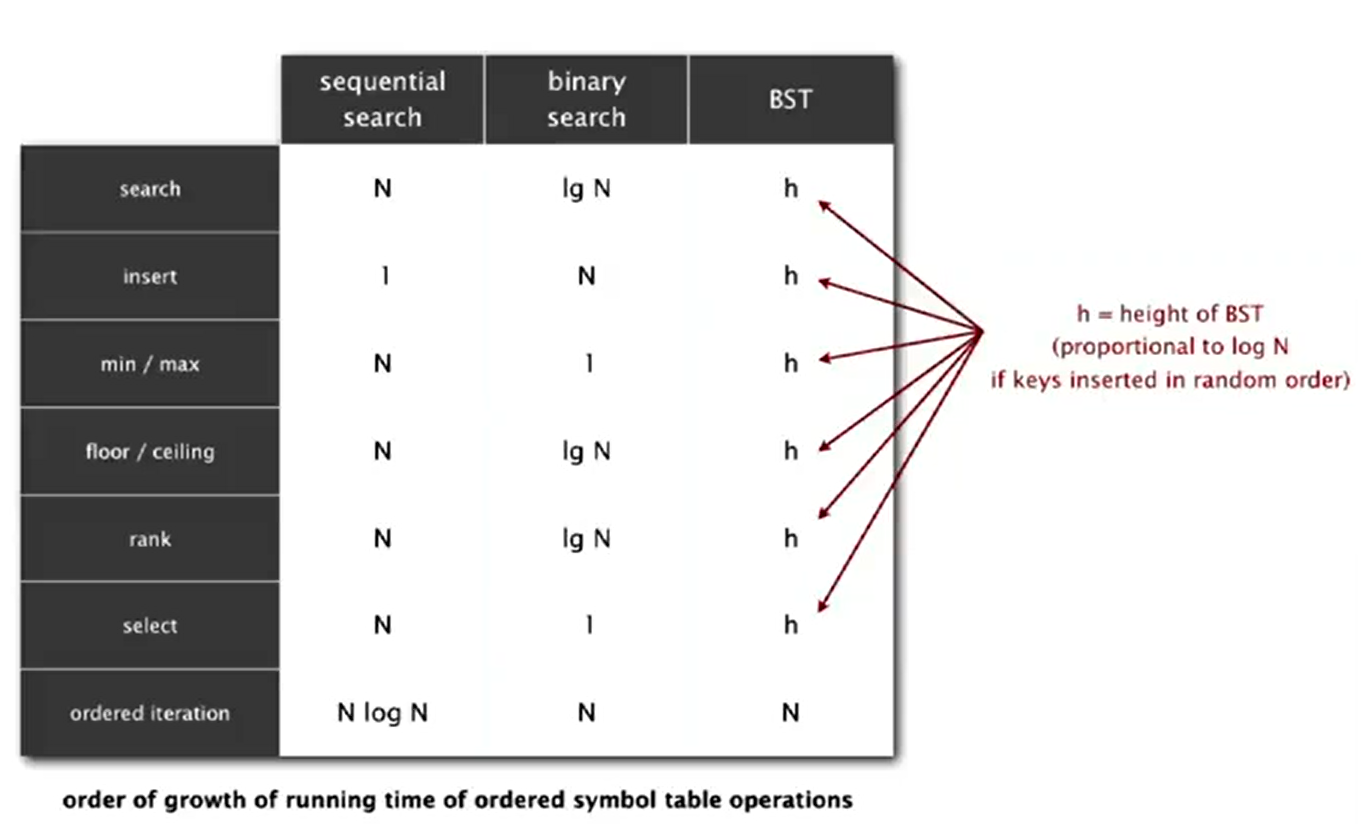
Balance Search Tree
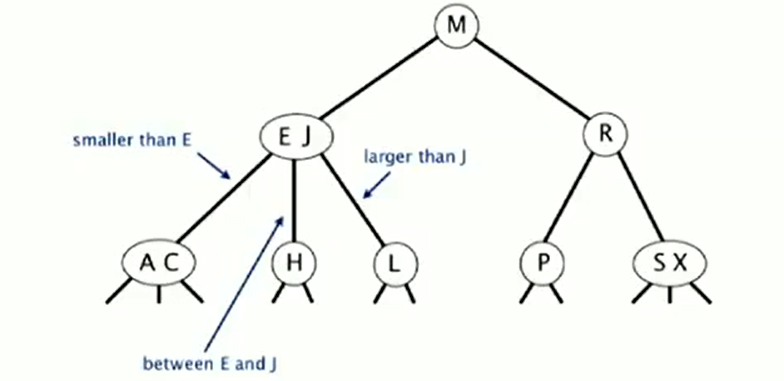
2-3 Search Tree
Perfect balance
Every path from root to null link has same length.Symmetric order
inoder traversal yields keys in ascending order.
Insert
Insert into a 2-node at bottom
- Search for key.
- Replace 2-node with 3-node
![image-20220926132043575]()
image-20220926132043575 ![image-20220926132206184]()
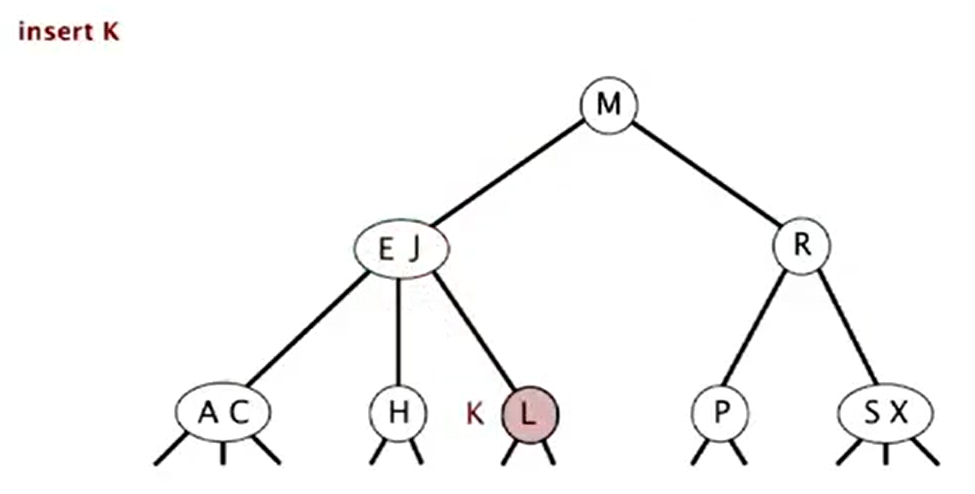
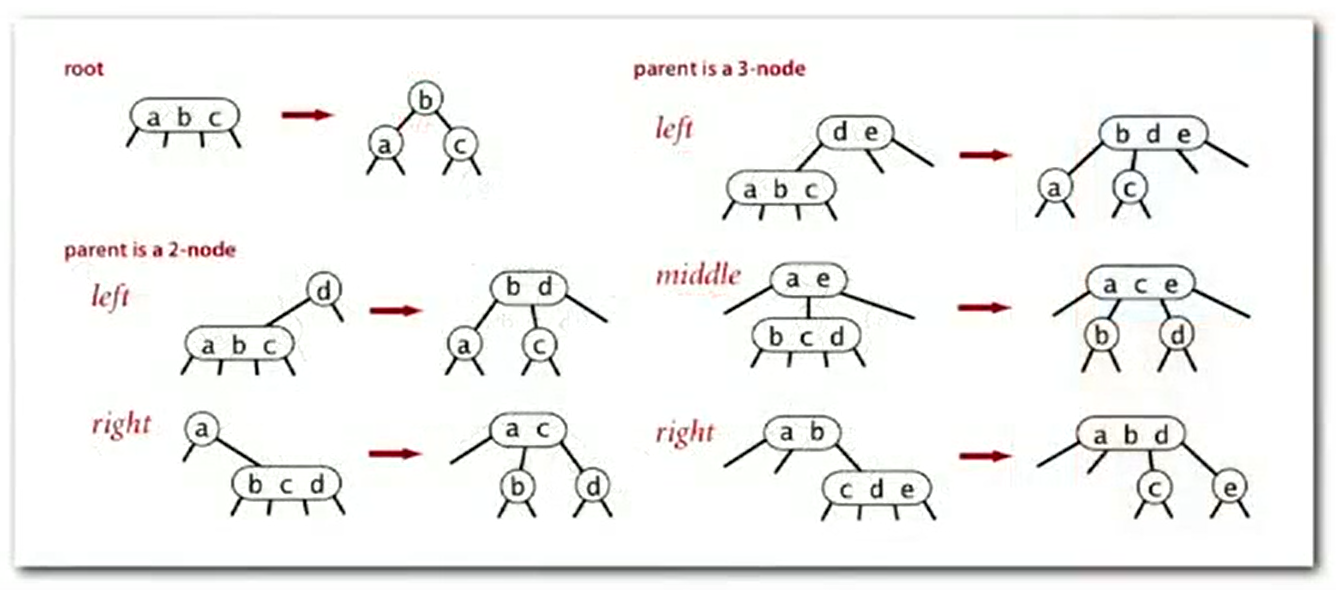
Insert into a 3-node at bottom
- Add new key to 3-node to create temporary 4-node
- Move middle key in 4-node into parent
![image-20220926132324553]()
image-20220926132324553 ![image-20220926132344007]()
image-20220926132344007 ![image-20220926132411904]()
Summary
![image-20220926132541204]()
image-20220926132541204
Performance
- Worst case:
lg N - Best case:
log3 N
Red-black Tree
- Represent 2-3 tree as a BST
- Use “internal” left-leaning links as “glue” for 3-nodes.
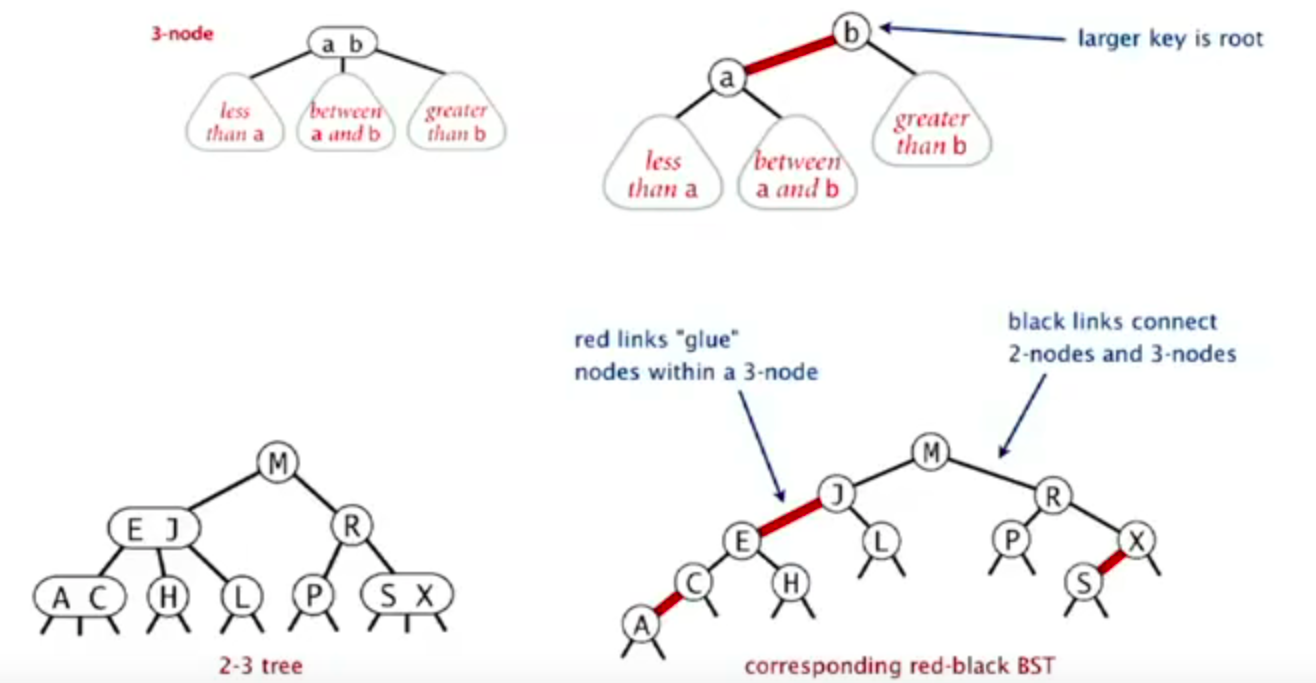
- No node has two red links connected to it.
- Every path from root to null link has the same number of black links.
- Red links lean left.
search
Search is the same as for elementary BST (ignore color).
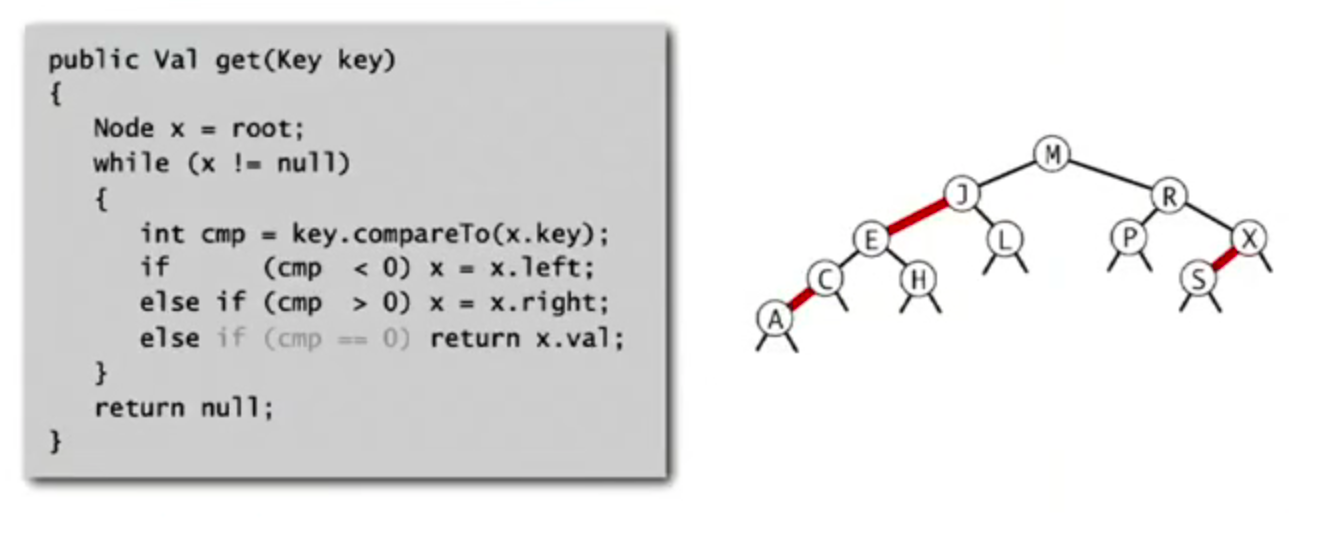
Representation
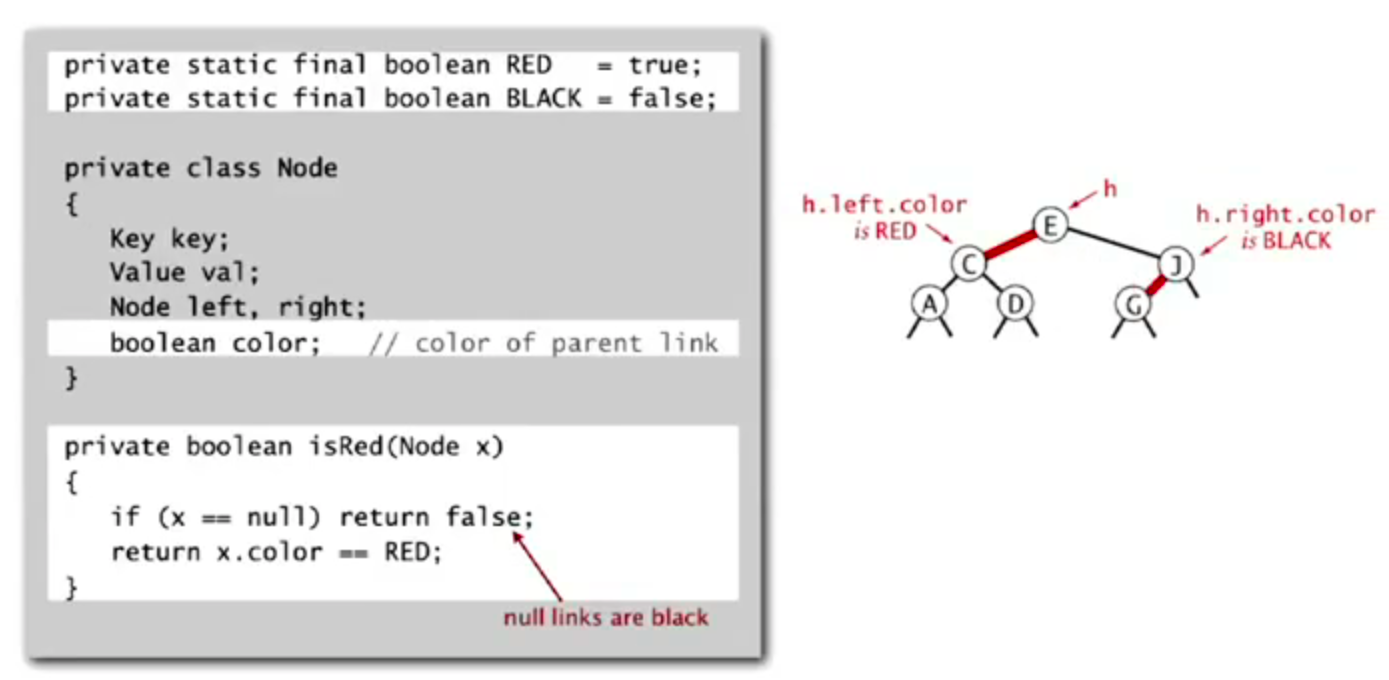
Operations
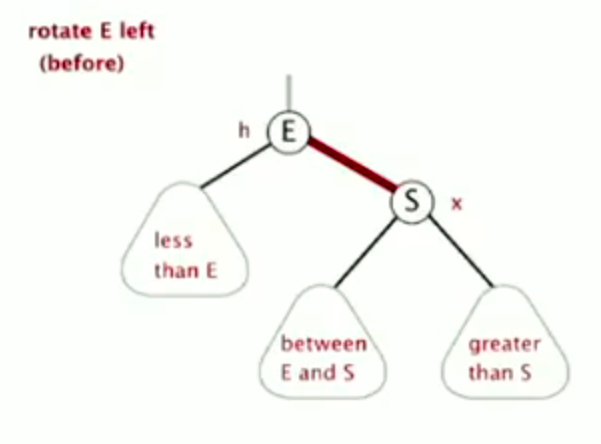
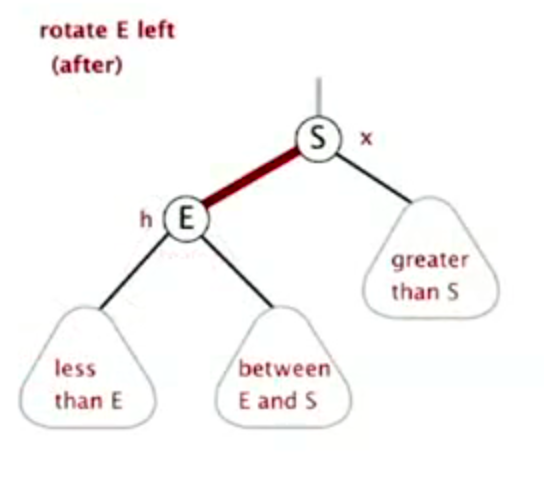
Left rotation
![image-20220926151732206]()
image-20220926151732206 ![image-20220926151746431]()
image-20220926151746431 ![image-20220926151759266]()
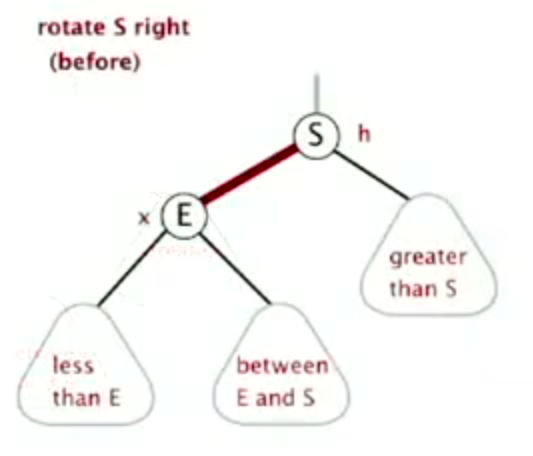
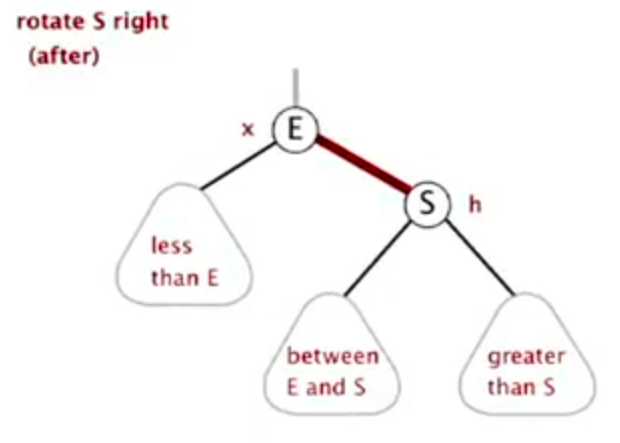
Right rotation
![image-20220926151845637]()
image-20220926151845637 ![image-20220926151858743]()
image-20220926151858743 ![image-20220926151908383]()
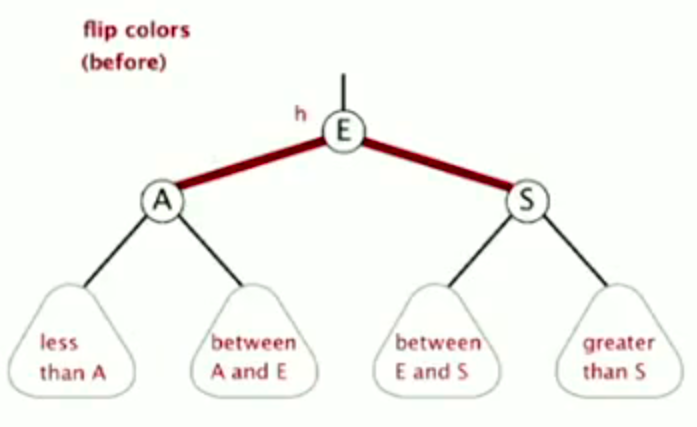
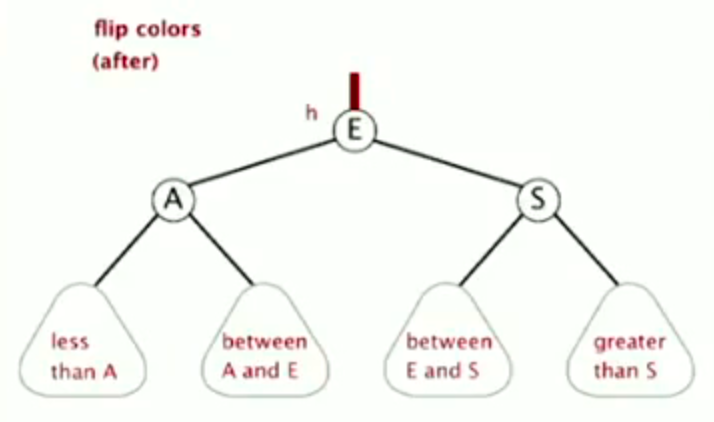
Color flip
![image-20220926151929745]()
image-20220926151929745 ![image-20220926151944111]()
image-20220926151944111 ![image-20220926151954953]()
image-20220926151954953
Strategy
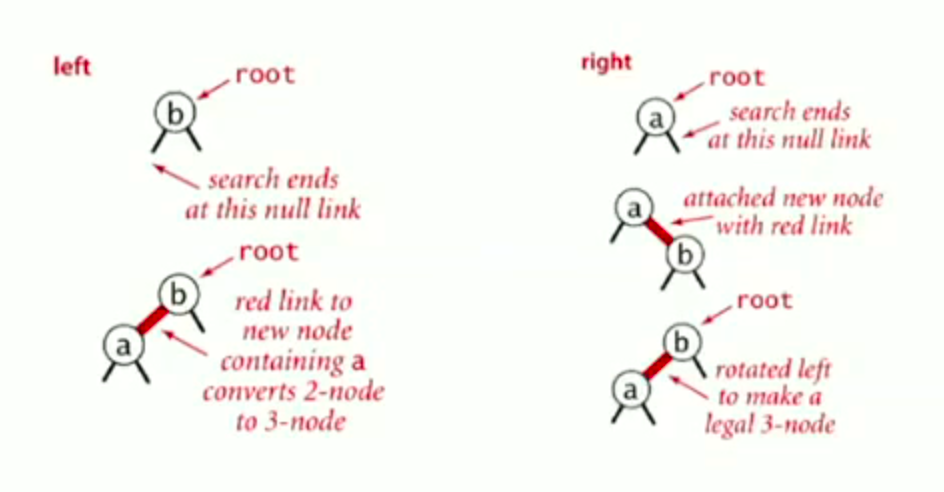
Insert into a tree with exactly 1 node.
![image-20220926152244170]()
Insert into a tree with exactly 2 nodes.
![image-20220926152420871]()
image-20220926152420871
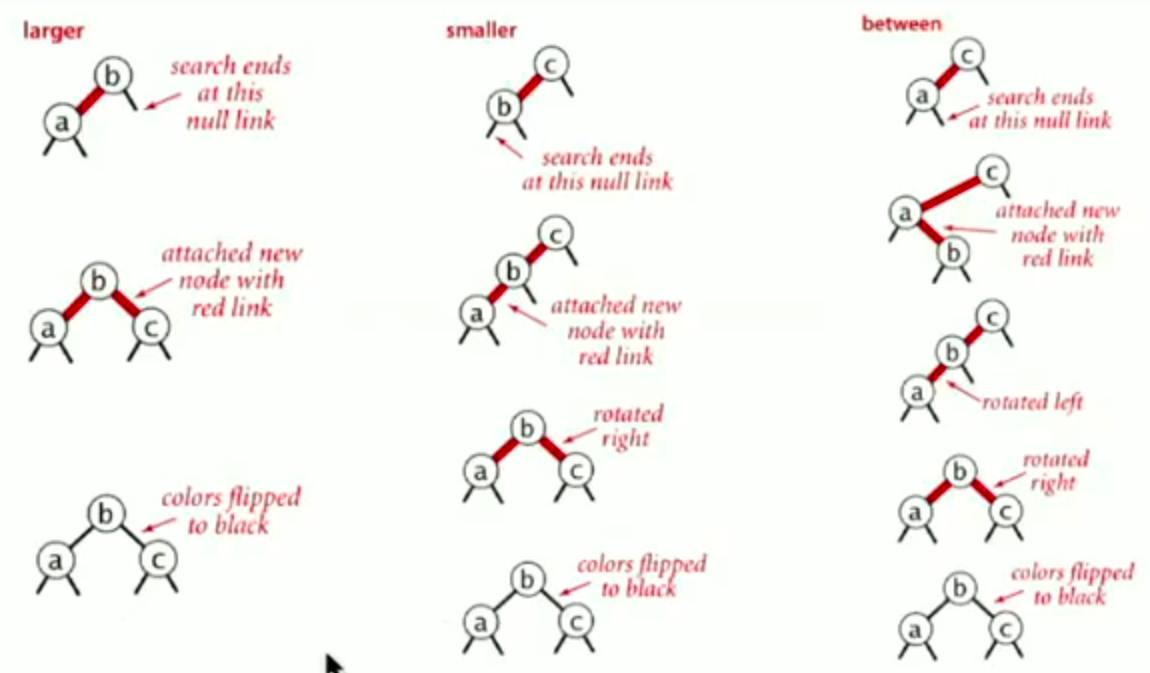
Implementation
- Right child red, left child black:
rotate left - Left child, left-left grandchild red:
rotate right - Both children red:
flip colors

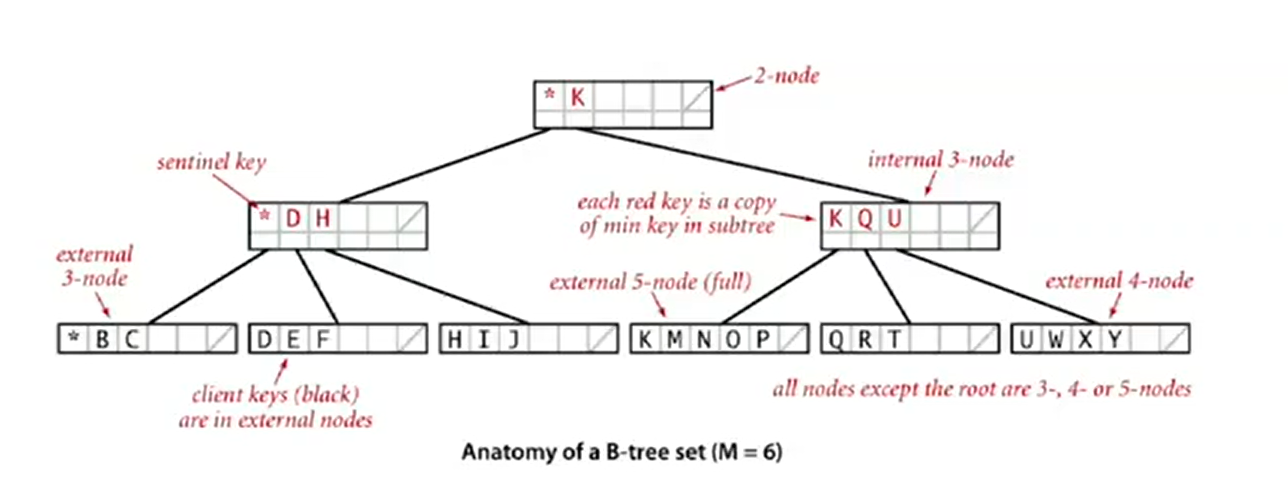
B-trees
- At least 2 key-link pairs in other nodes.
- At least M/2 key-link pairs in other nodes.
- External nodes contain client keys.
- Internal nodes contain copies of keys to guide search.
我怎么觉得这是 B + 树(我也不懂啊)。。。
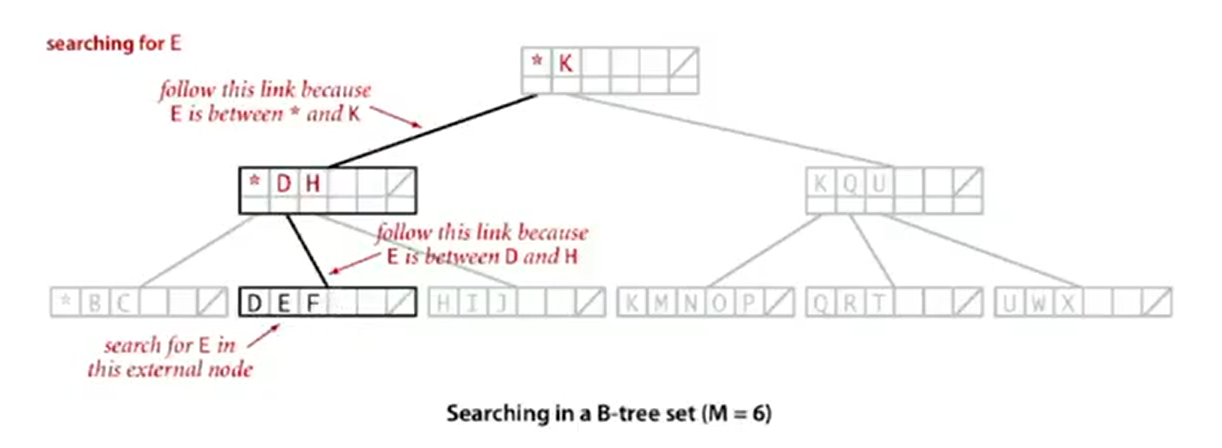
Search
- Start at root.
- Find interval for search key and take corresponding link.
- Search terminates in external node.
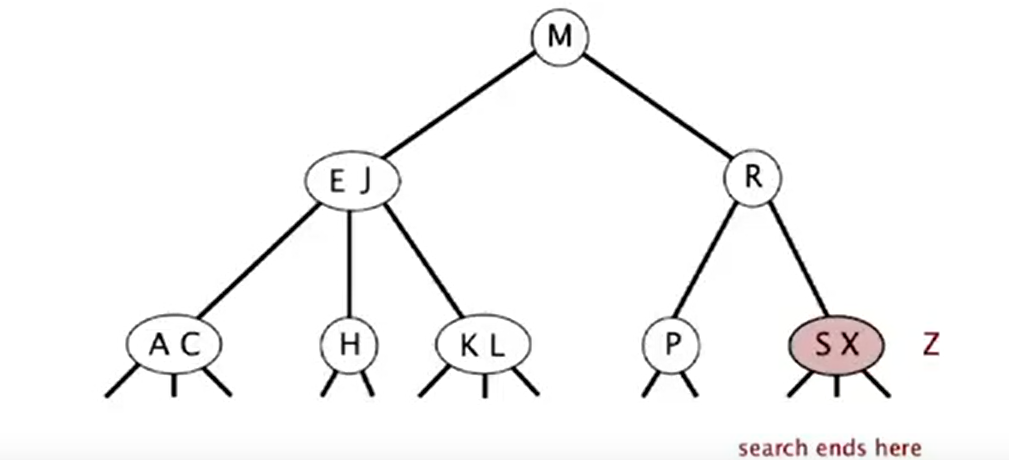
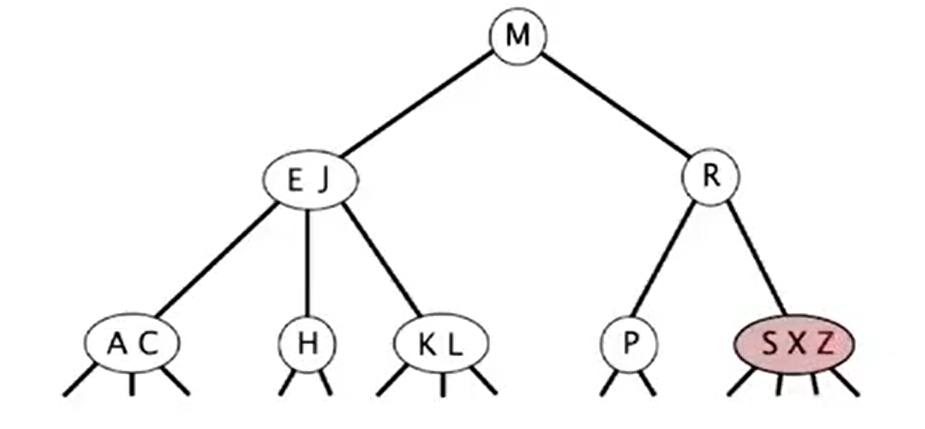
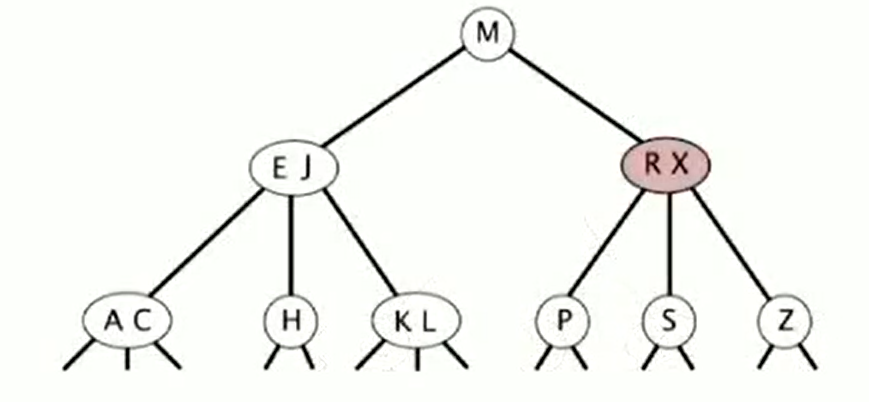
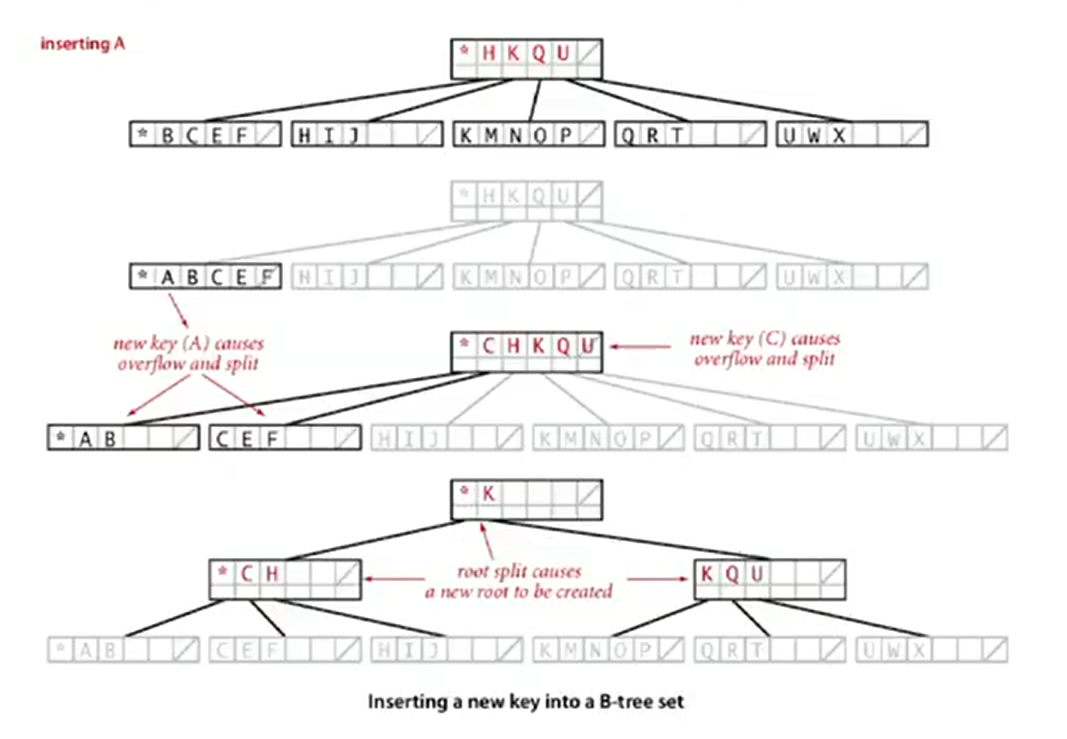
Insertion
- Search for new key.
- Insert at bottom.
- Split nodes with M key-link pairs on the way up the tree.
Geometric Appliations of BSTs
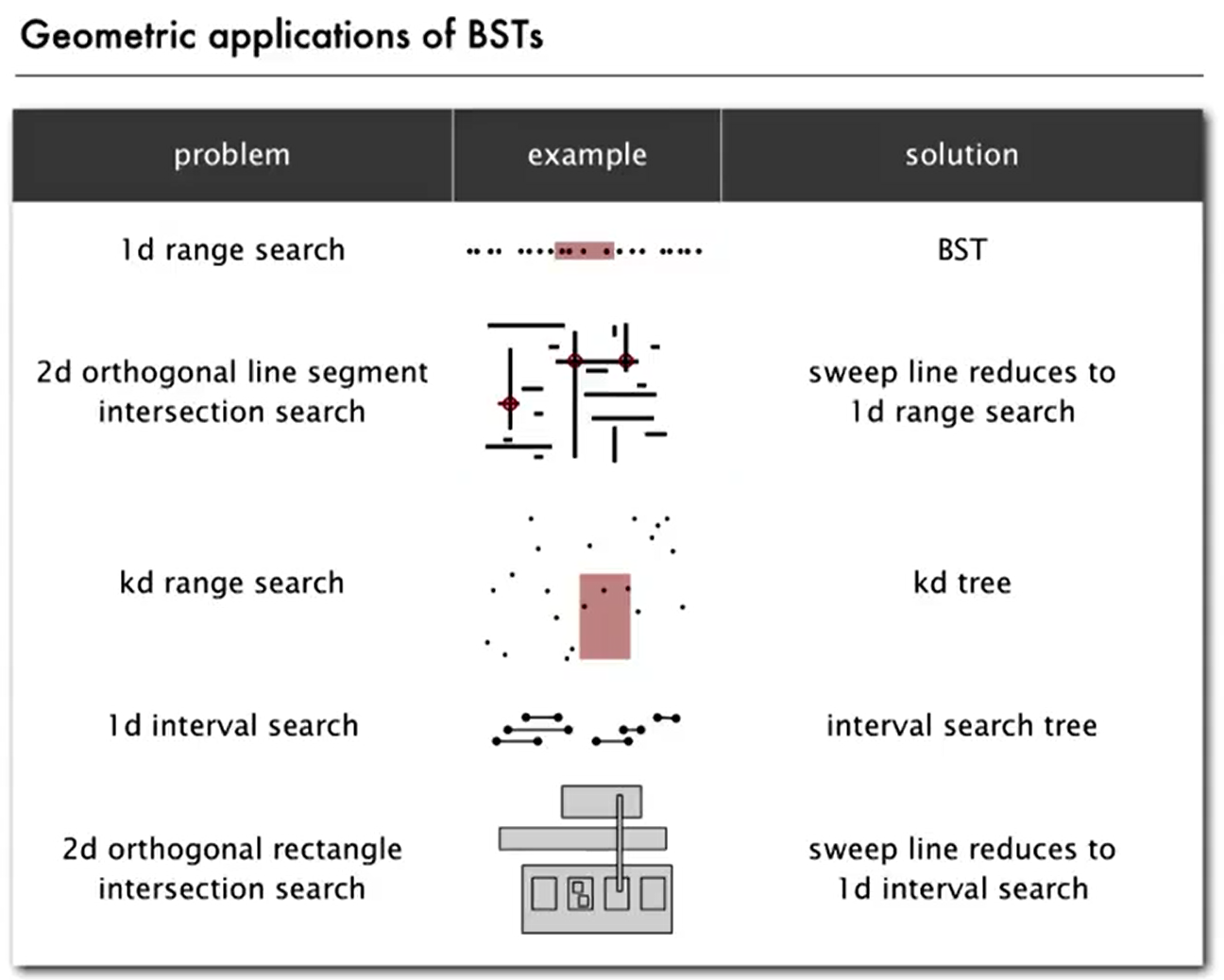
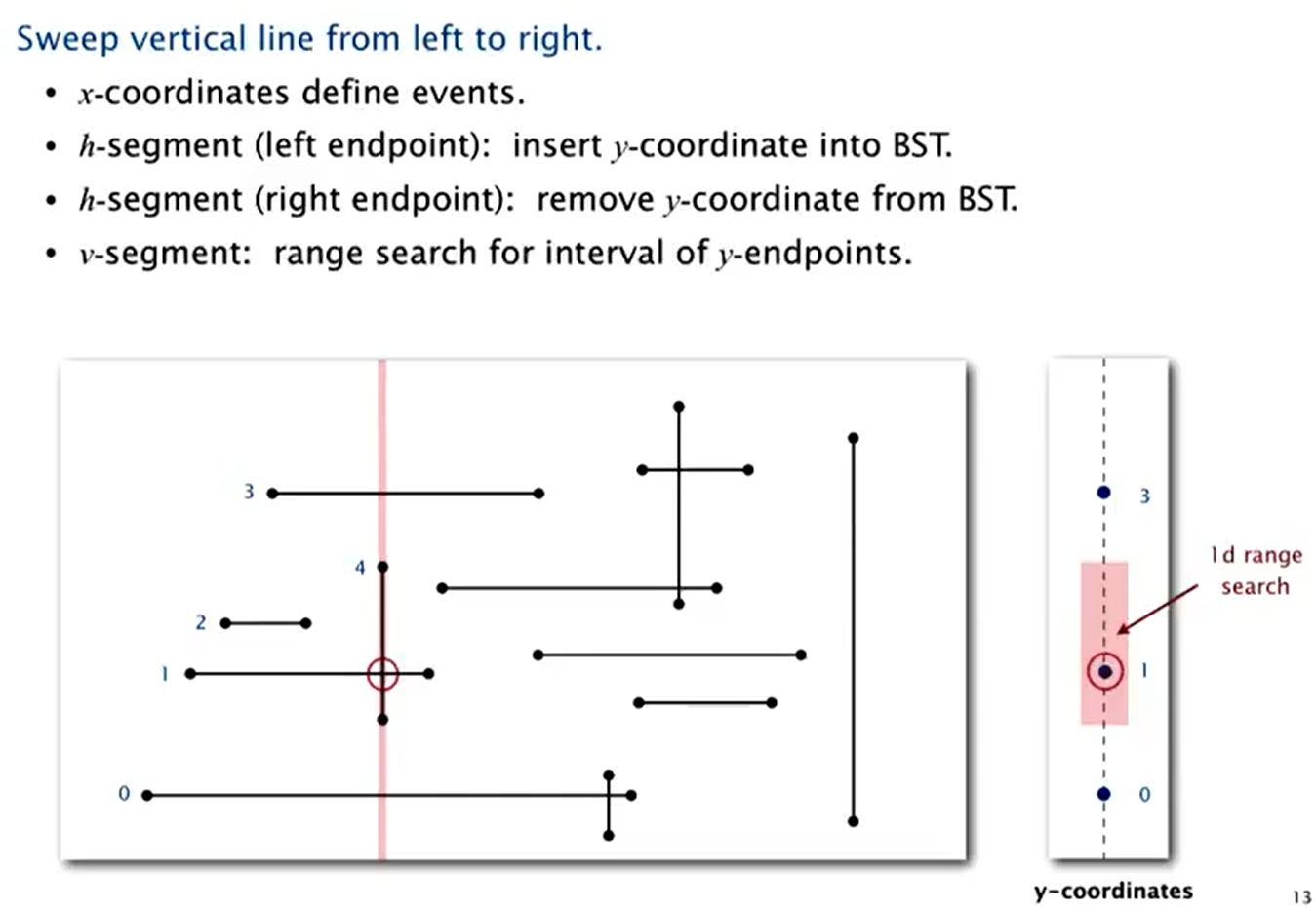
1d range search
Task
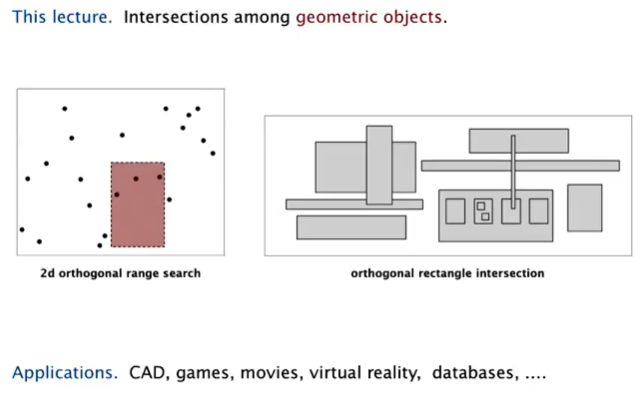
Goal

BST implementation
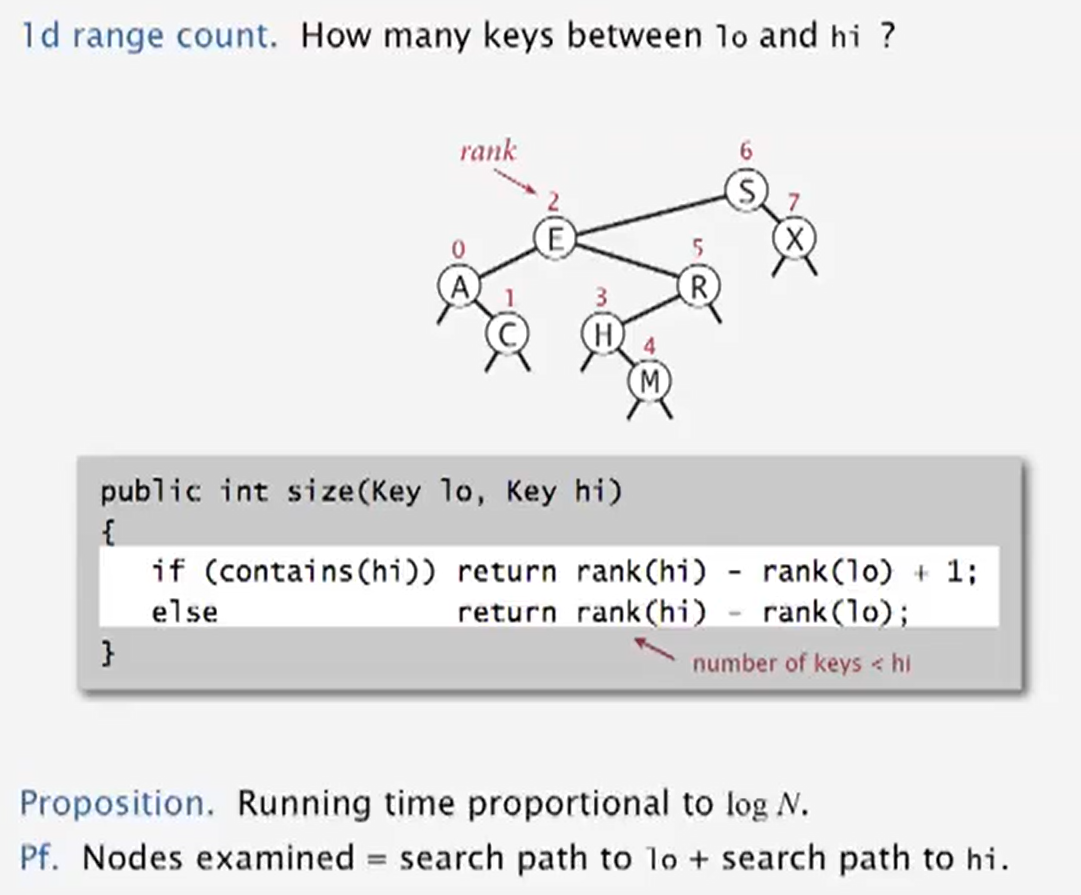
Line segment intersection
KD-Trees
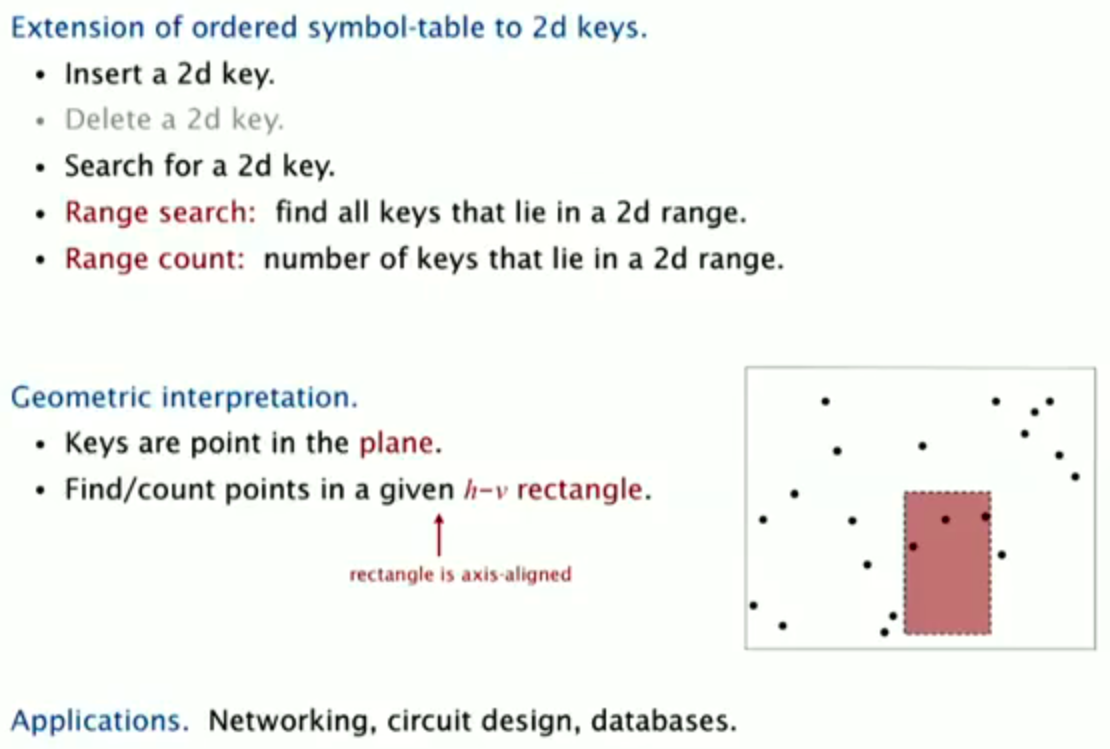
2-d orthogonal range search

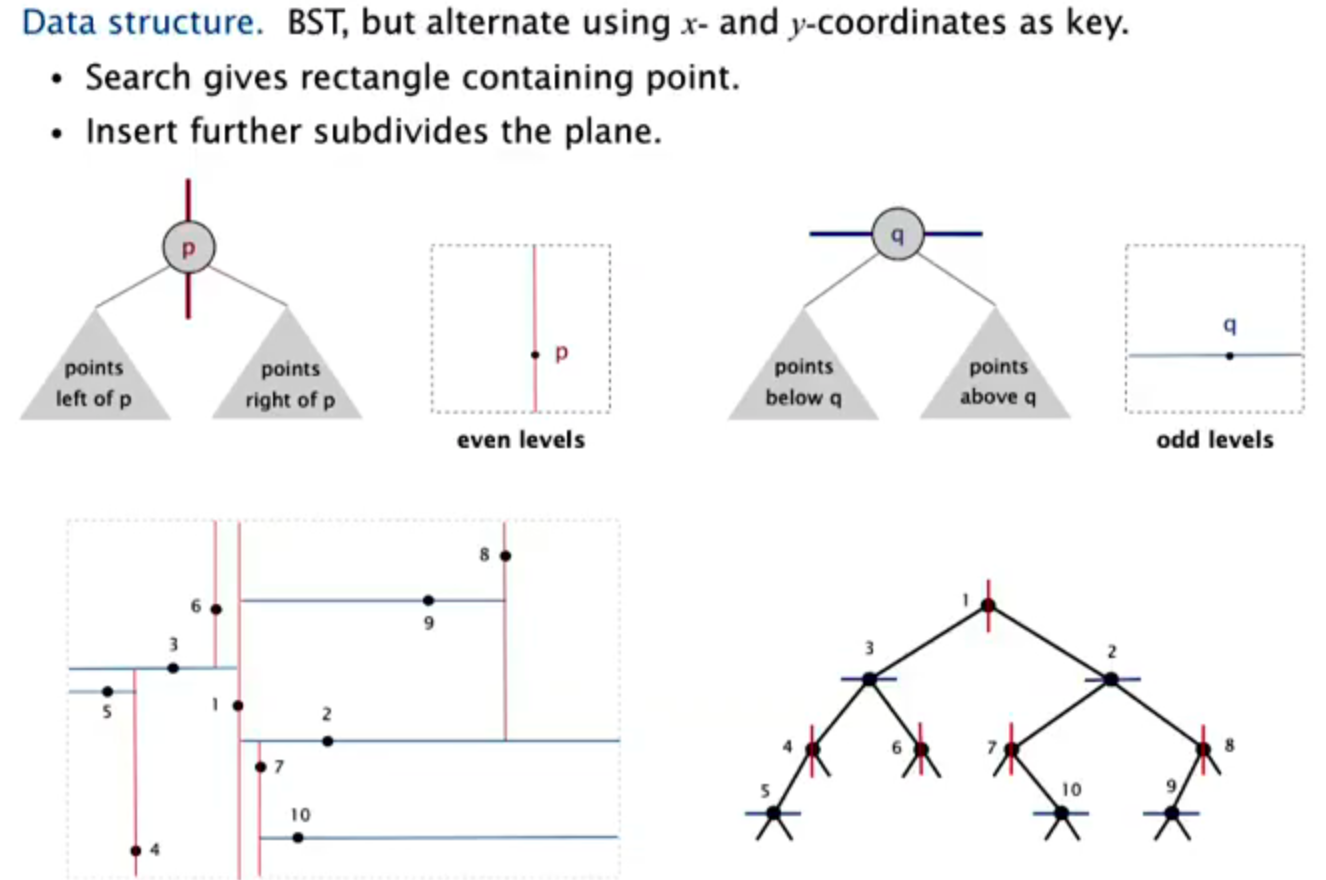
Implementation
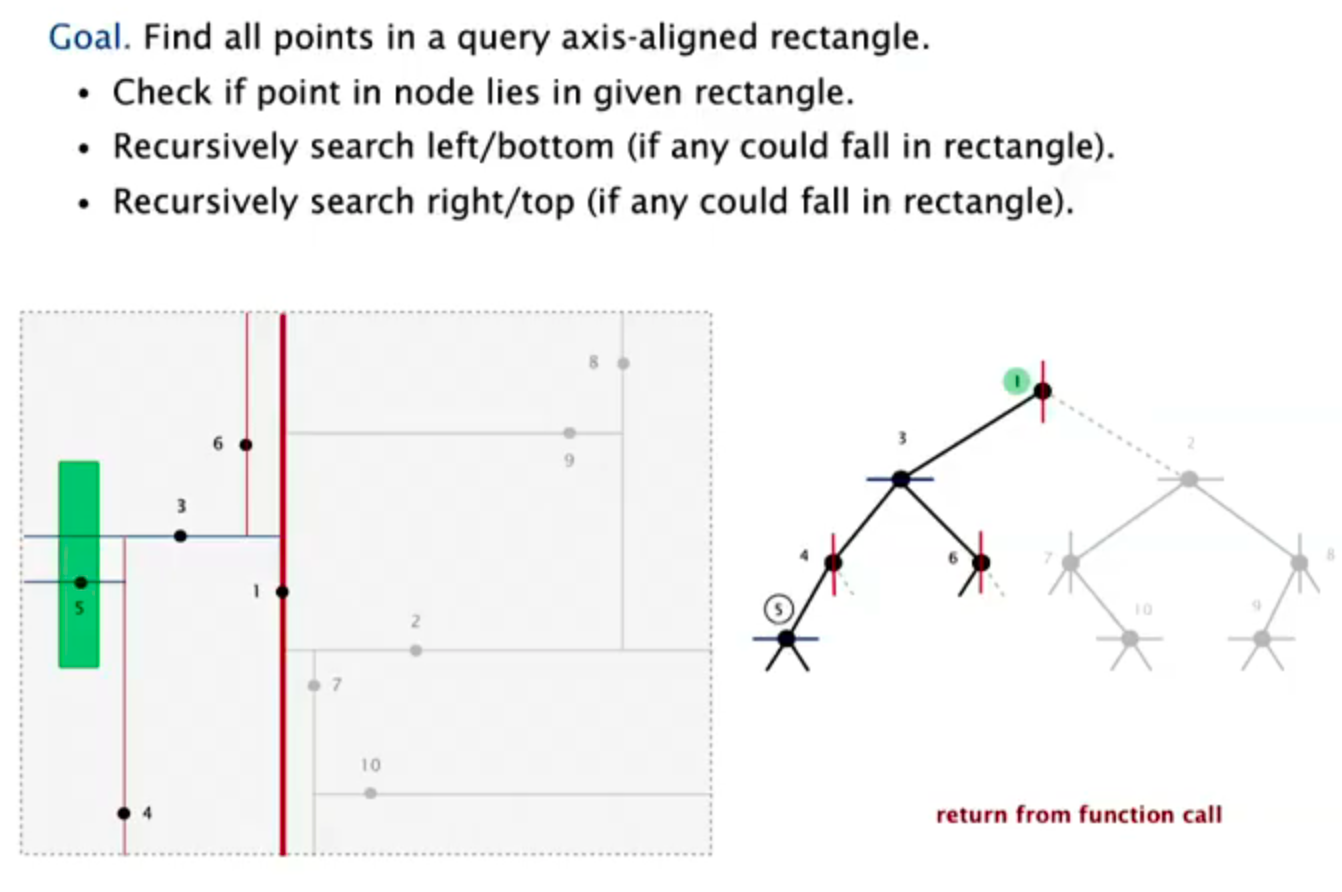
Range search
Typical case: R + logN
Worst case (assuming tree is balanced): R + N^(1/2)
Nearest neighbor search
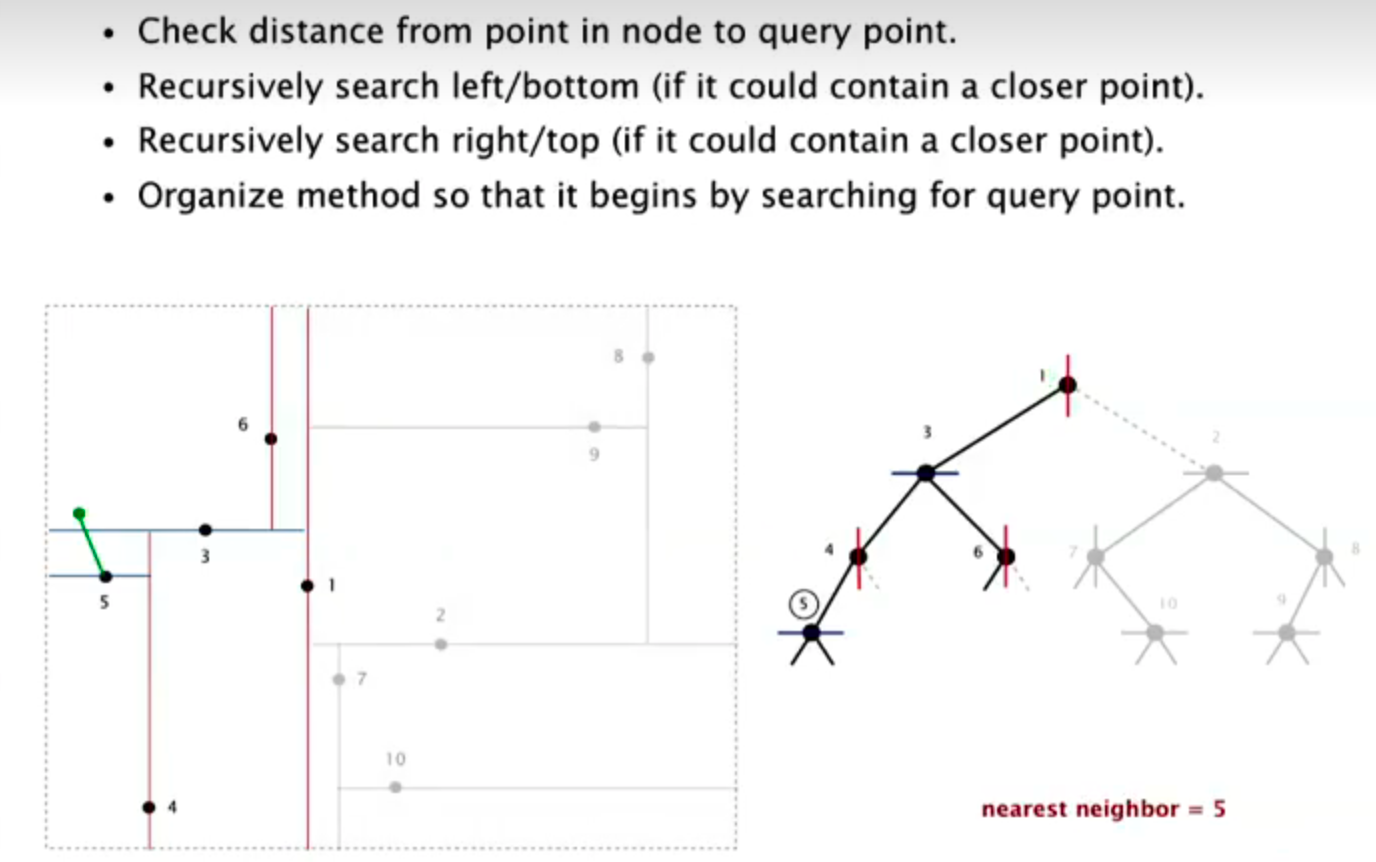
Typical case: logN
Worst case (even if tree is balanced): N
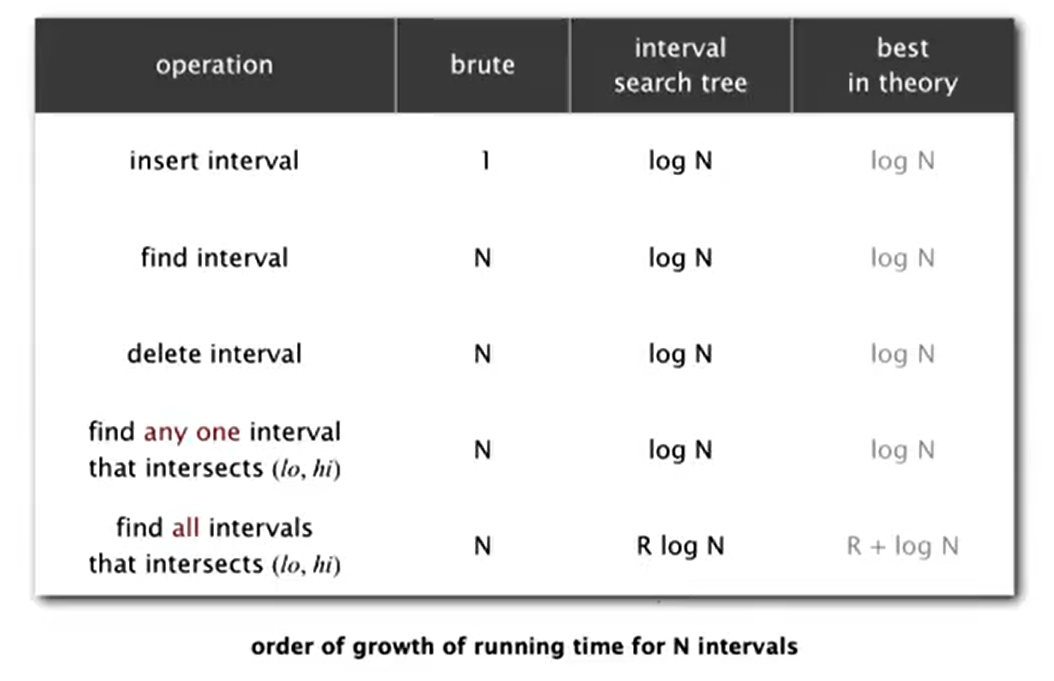
Interval search trees
1d interval search

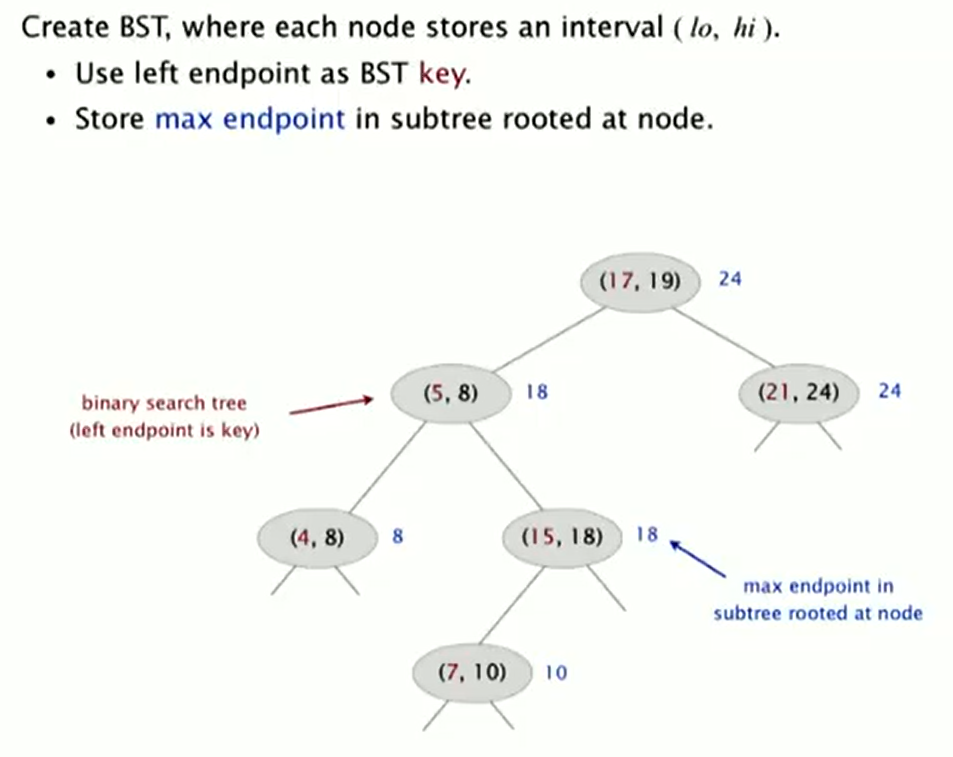
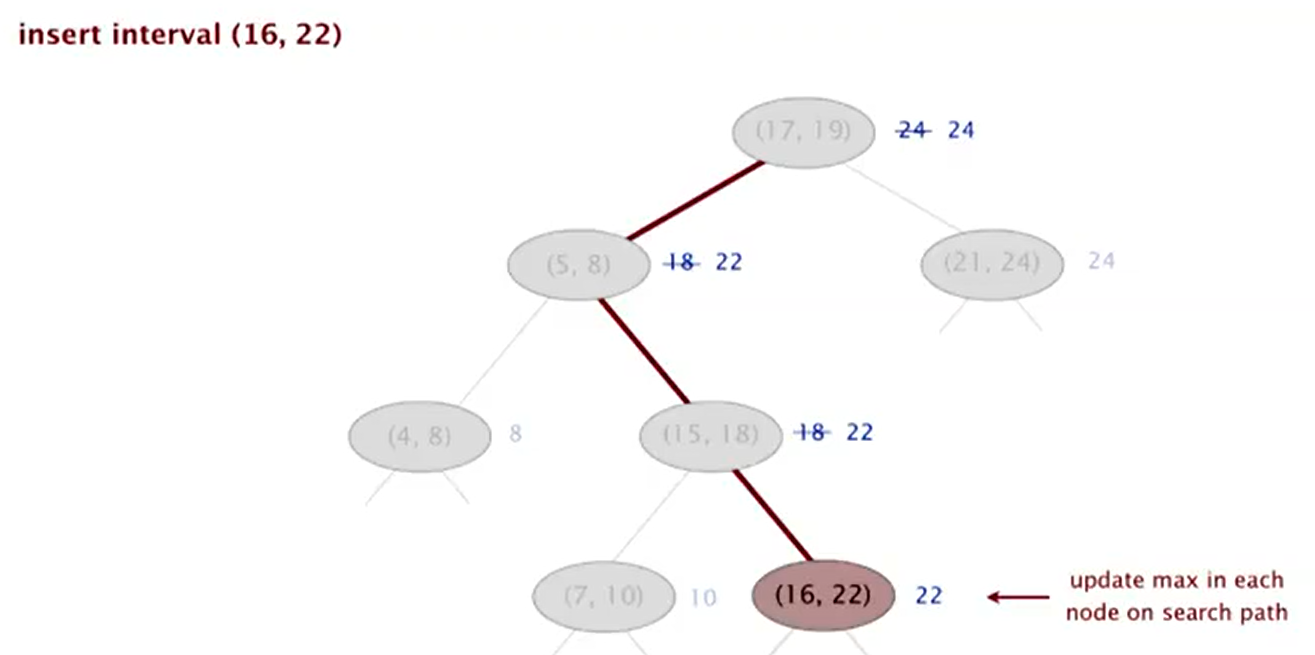
Insert
To insert an interval (lo, hi):
- Insert into BST, using lo as the key.
- Update max in each node on search path.
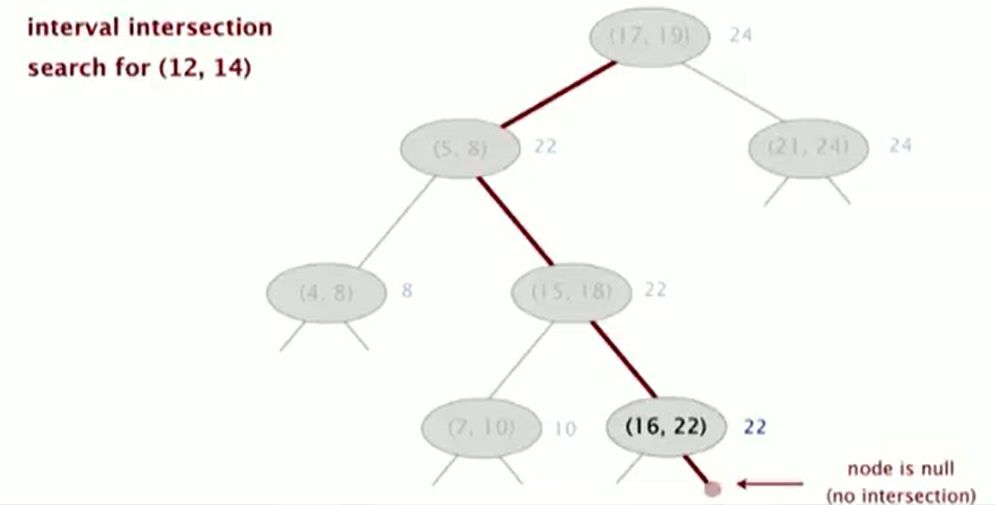
Search
To search for any one interval that intersects query interval (lo, hi):
- If interval in node intersects query interval, return it.
- Else if left subtrees is null, go right.
- Else if max endpoint in left subtrees is less than lo, go right.
- Else go left.
Inplementation
Use a RB BST to guarantee performance.
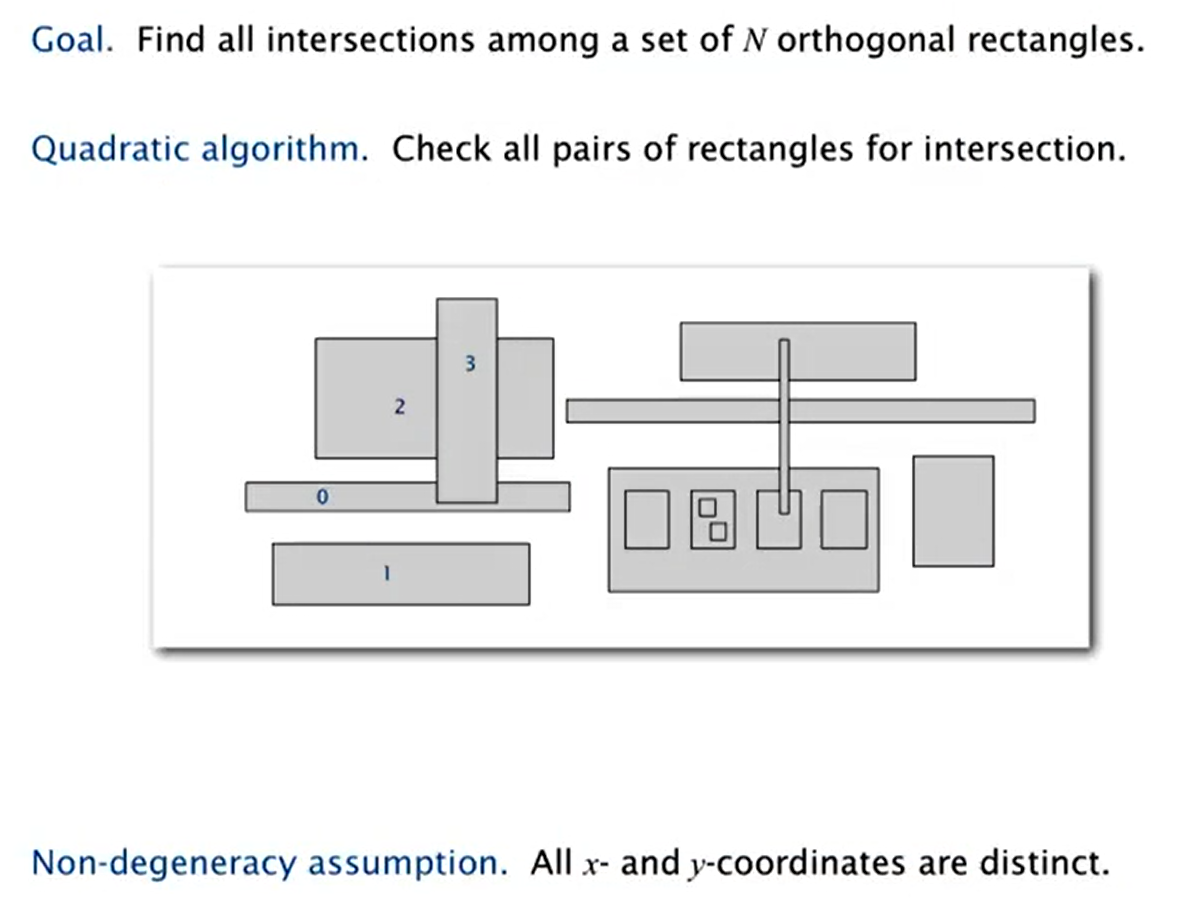
Rectangle Intersection
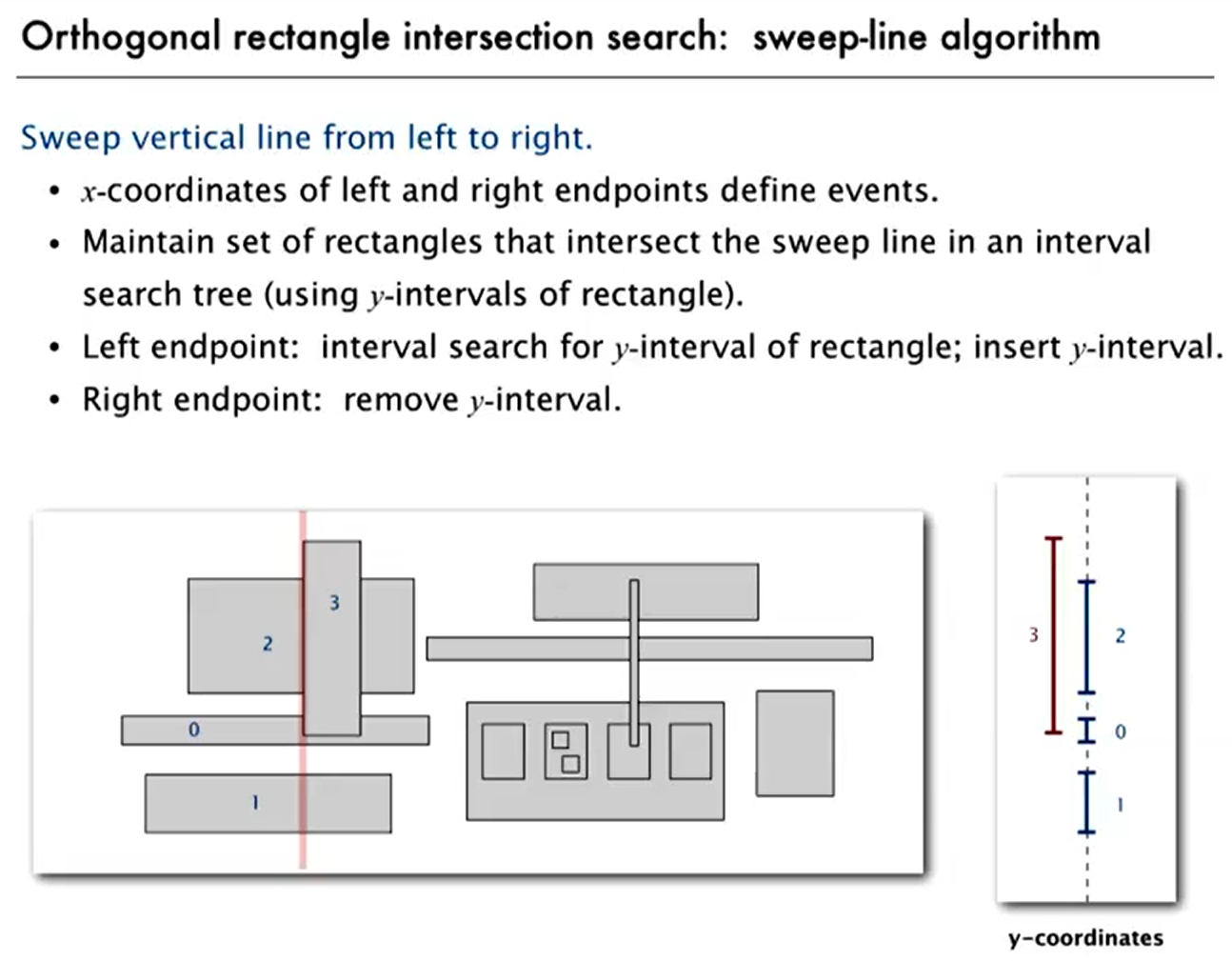
(x 维换到时间维度,转换到 1d 问题了?)

Hash table
Hash function
Method for computing array index from key.


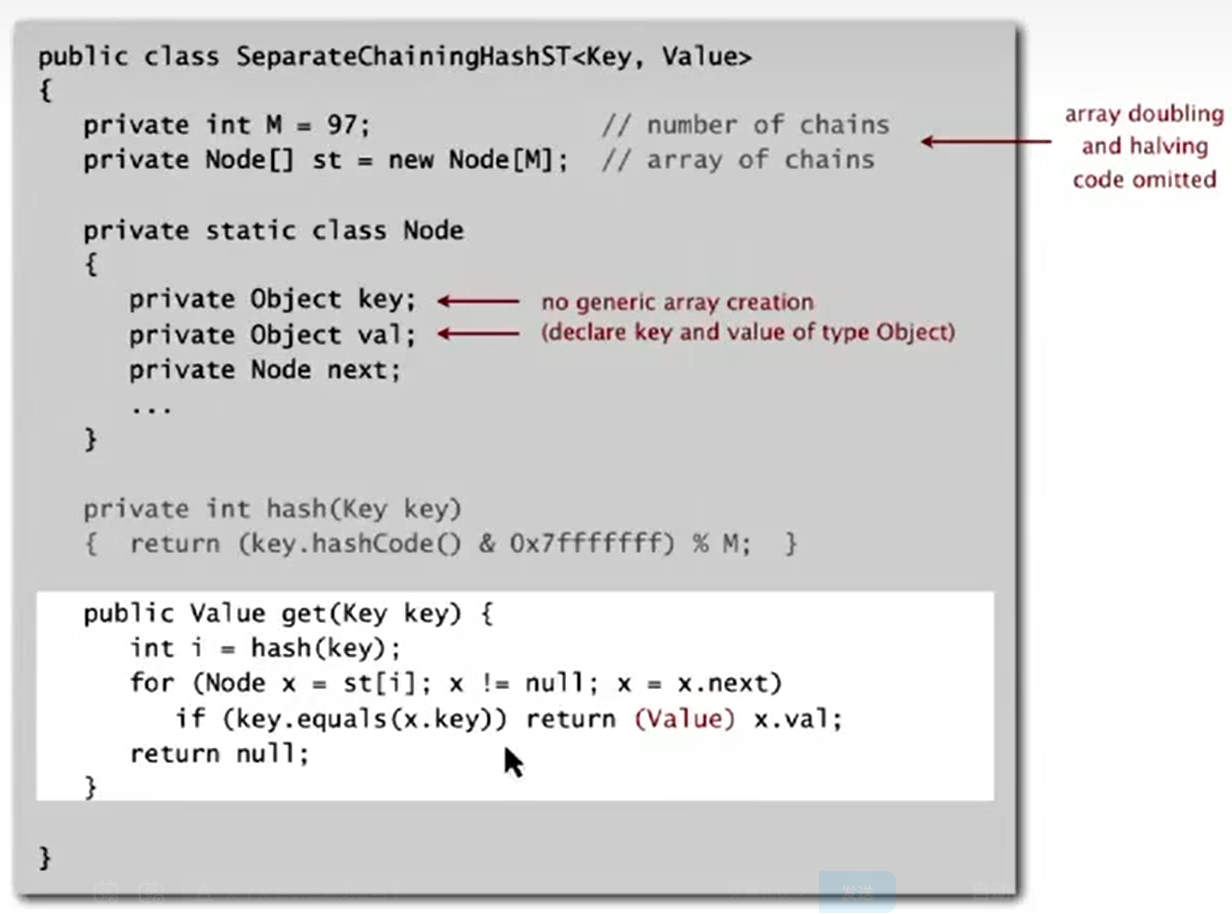
Separate Chaining
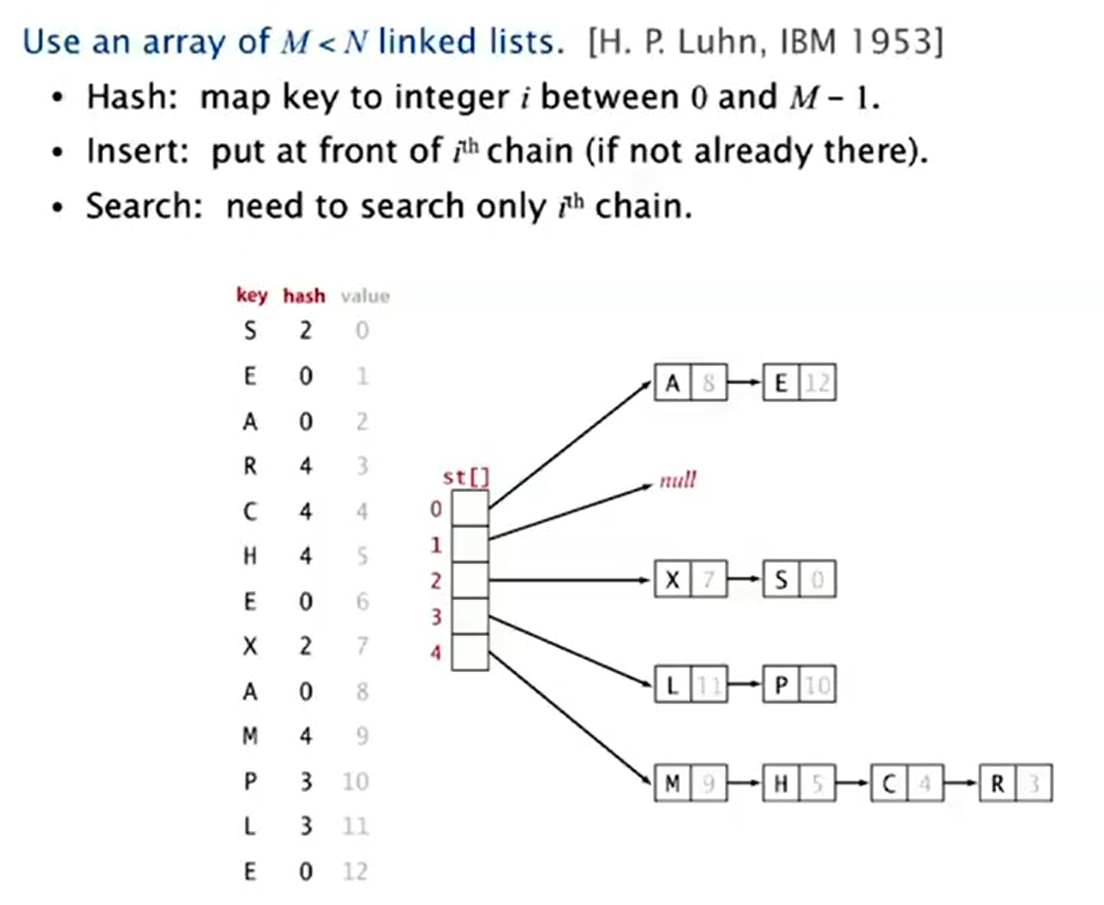
Implementation
get
![1664454550102]()
put
![1664454595670]()
1664454595670
Analysis

Linear Probing
- Hash. Map key to integer
ibetween 0 and M-1. - Insert. Put at table index
iif free; if not tryi+1,i+2, etc. - Search. Search table index
i; if occupied but no match, tryi+1,i+2, etc. - Note. Array size M must be greater than number of key-value pairs N.
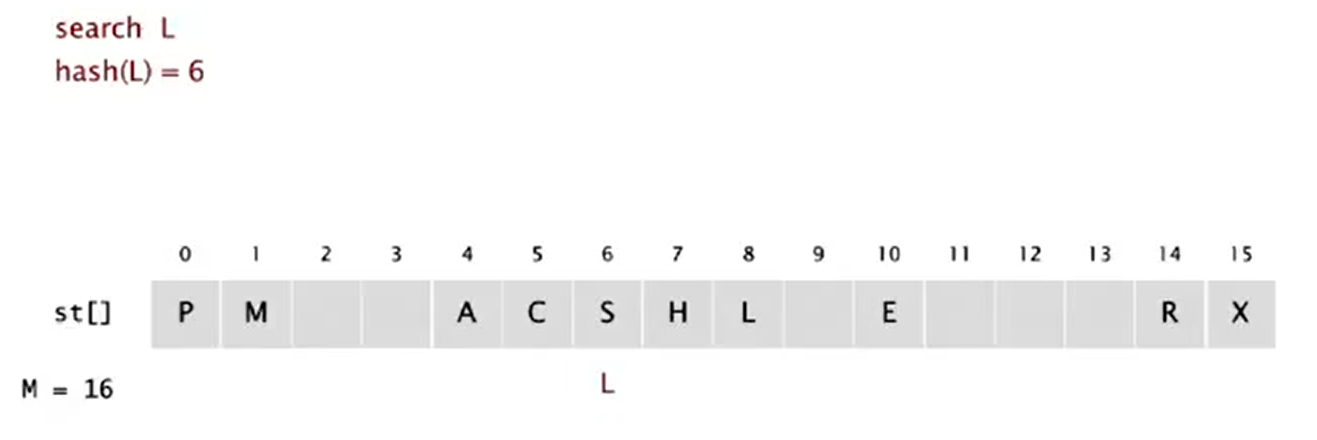
Impletementation
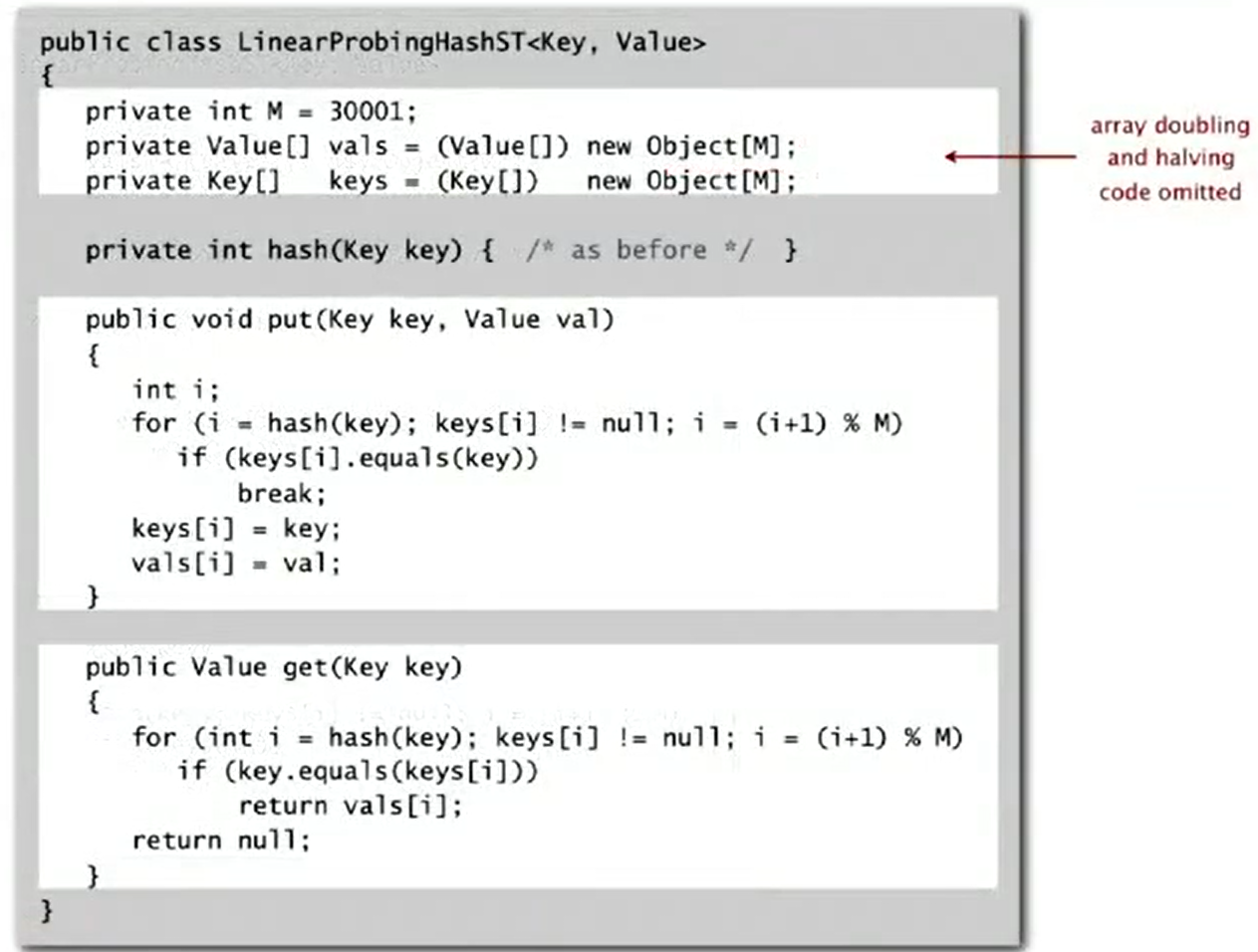
Analysis


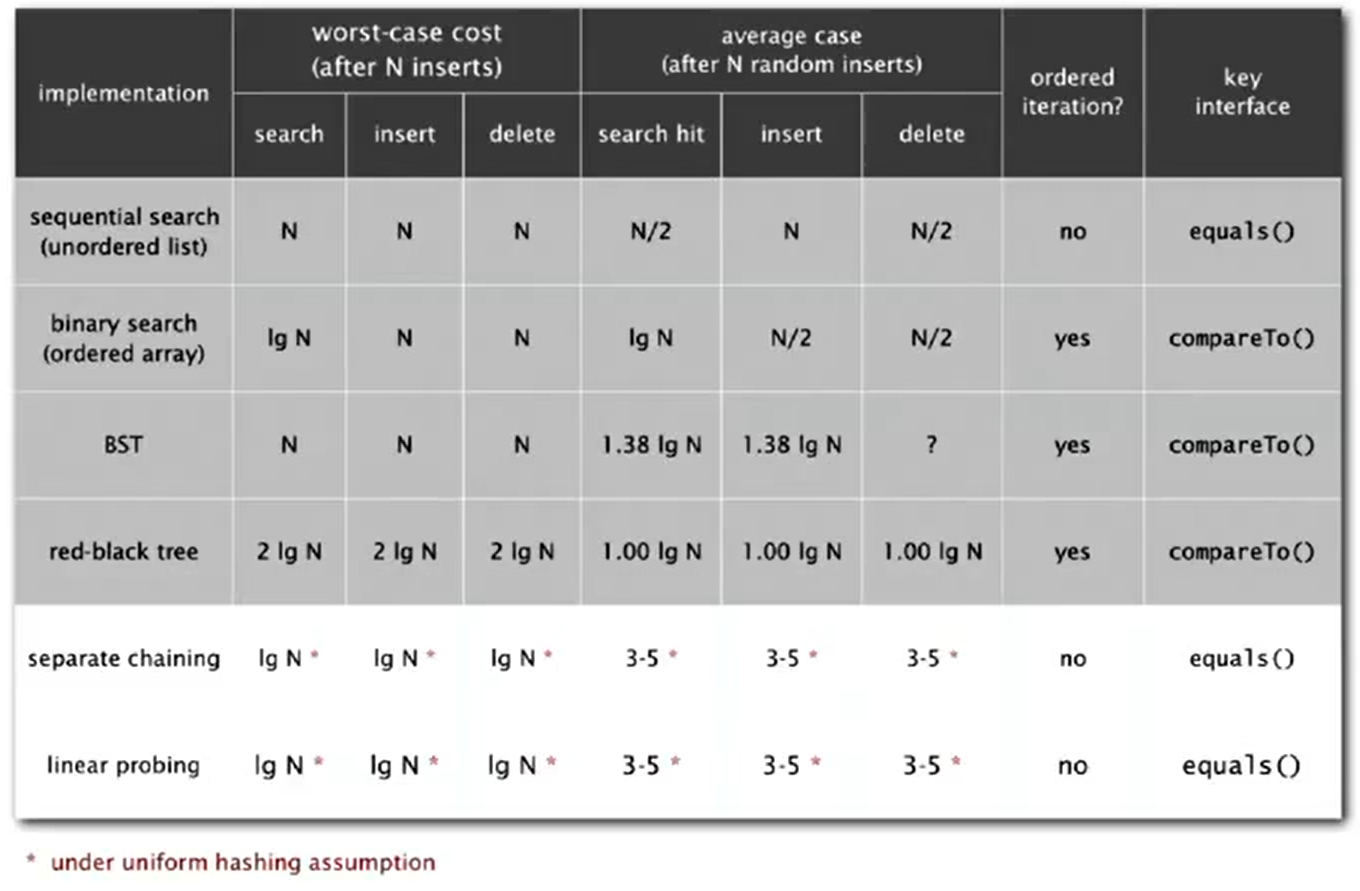
Context